 por matheu_chaves » Seg Dez 20, 2010 17:48
por matheu_chaves » Seg Dez 20, 2010 17:48
como provar que todo numero da forma
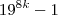
é divisivel por 17.estou tentando pelo metodo de indução matematica mas não consigo representar o polinomio do (k+1)-enesimo termo e fatora-lo.me ajudem por favor.
-
matheu_chaves
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Dez 15, 2010 15:41
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: PIC-2009
- Andamento: cursando
 por davi_11 » Ter Dez 21, 2010 11:46
por davi_11 » Ter Dez 21, 2010 11:46
"Se é proibido pisar na grama, o jeito é deitar e rolar..."
-
davi_11
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Sex Abr 02, 2010 22:47
- Localização: Leme - SP
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso técnico em eletrotécnica
- Andamento: formado
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Provar se é par
por stalone » Seg Dez 21, 2009 23:29
- 5 Respostas
- 3239 Exibições
- Última mensagem por stalone

Seg Dez 13, 2010 13:07
Desafios Difíceis
-
- Provar que ||u|| > 0
por 0 kelvin » Qui Mar 24, 2011 20:35
- 2 Respostas
- 1989 Exibições
- Última mensagem por 0 kelvin

Qui Mar 24, 2011 21:16
Geometria Analítica
-
- Provar
por scggomes » Sex Abr 15, 2011 16:38
- 8 Respostas
- 5973 Exibições
- Última mensagem por MarceloFantini

Sáb Abr 16, 2011 15:56
Cálculo para Funções de Uma Variável Real I
-
- provar que
por anamendes » Ter Jun 19, 2012 07:41
- 1 Respostas
- 1428 Exibições
- Última mensagem por fraol

Qua Jun 20, 2012 21:19
Trigonometria
-
- Provar
por Jovani Souza » Ter Jun 11, 2013 21:03
- 0 Respostas
- 1028 Exibições
- Última mensagem por Jovani Souza

Ter Jun 11, 2013 21:03
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
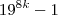 é divisivel por 17.estou tentando pelo metodo de indução matematica mas não consigo representar o polinomio do (k+1)-enesimo termo e fatora-lo.me ajudem por favor.
é divisivel por 17.estou tentando pelo metodo de indução matematica mas não consigo representar o polinomio do (k+1)-enesimo termo e fatora-lo.me ajudem por favor.

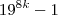 é divisivel por 17.estou tentando pelo metodo de indução matematica mas não consigo representar o polinomio do (k+1)-enesimo termo e fatora-lo.me ajudem por favor.
é divisivel por 17.estou tentando pelo metodo de indução matematica mas não consigo representar o polinomio do (k+1)-enesimo termo e fatora-lo.me ajudem por favor.
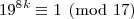
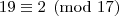
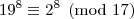
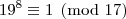
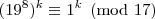
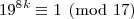 c.q.d.
c.q.d.