 por Manoella » Qui Dez 16, 2010 09:44
por Manoella » Qui Dez 16, 2010 09:44
Olá! Preciso que alguém mim explica sobre essas integrais ai;
a)
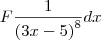
b)
![\int_{1}^{-1}\frac{{x}^{2}}{\sqrt[]{{x}^{3}+9}}dx \int_{1}^{-1}\frac{{x}^{2}}{\sqrt[]{{x}^{3}+9}}dx](/latexrender/pictures/4619b465be8533ed1053444897a04054.png)
-
Manoella
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Qui Dez 16, 2010 09:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por Moura » Qui Dez 16, 2010 10:54
por Moura » Qui Dez 16, 2010 10:54
P = NP
-
Moura
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Seg Dez 13, 2010 11:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
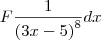
![\int_{1}^{-1}\frac{{x}^{2}}{\sqrt[]{{x}^{3}+9}}dx \int_{1}^{-1}\frac{{x}^{2}}{\sqrt[]{{x}^{3}+9}}dx](/latexrender/pictures/4619b465be8533ed1053444897a04054.png)

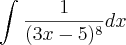
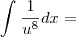
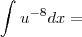
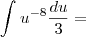
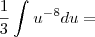
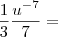
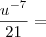
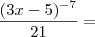
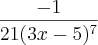

![\int_{1}^{-1}\frac{x^2}{\sqrt[]{x^3+9}}dx = \int_{1}^{-1}\frac{x^2}{\sqrt[]{x^3+9}}dx =](/latexrender/pictures/2c31b51a4a33f7a070ffee6fcc231de1.png)
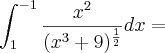
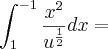
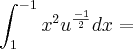
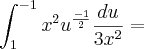
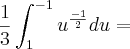
![\frac{1}{3}\frac{u^\frac{1}{2}}{\frac{1}{2}}]_{1}^{-1} = \frac{1}{3}\frac{u^\frac{1}{2}}{\frac{1}{2}}]_{1}^{-1} =](/latexrender/pictures/5332381d849797b972bab1e6c9c4dbfd.png)
![\frac{2}{3}u^\frac{1}{2}]_{1}^{-1} = \frac{2}{3}u^\frac{1}{2}]_{1}^{-1} =](/latexrender/pictures/29604106ec2402520f1f69ab1d67a780.png)
![\frac{2(x^3+9)^\frac{1}{2}}{3}]_{1}^{-1} = \frac{2(x^3+9)^\frac{1}{2}}{3}]_{1}^{-1} =](/latexrender/pictures/83ecac203a7e16e6fd107e5b02fb72f7.png)
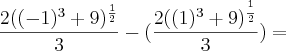
![\frac{4*\sqrt[]{2}}{3}-\frac{2*\sqrt[]{10}}{3} \frac{4*\sqrt[]{2}}{3}-\frac{2*\sqrt[]{10}}{3}](/latexrender/pictures/bcbf7f1459a900a94b3a7c5fb598374a.png)

