 por Lorettto » Seg Dez 13, 2010 01:34
por Lorettto » Seg Dez 13, 2010 01:34
Como faz esse ? Uma torneira enche um depósito d'água em 1/14 da hora enquanto uma válvula pode esvaziá-la em 1/19 da hora. Trabalhando juntas, em quanto tempo o líquido contido no depósito atingirá seus 5//6 ?
-
Lorettto
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Sáb Nov 27, 2010 01:17
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por PedroSantos » Seg Dez 13, 2010 04:05
por PedroSantos » Seg Dez 13, 2010 04:05
Vejamos, a torneira enche o depósito e a valvula esvazia-o.Logo
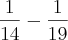
Pode-se verificar que
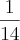
é maior que
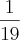
. Conclui-se que por cada unidade de tempo o depósito enche na diferença entre a torneira e a valvula.Seja
n a quantidade de tempo.
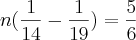
Julgo que é assim, pois (conforme o enunciado) a torneira enche em 1/14 de hora (4 min 17seg) e a valvula esvazia em 1/19 de hora (3 min 10seg). Nesta perspectiva a valvula esvazia mais depressa do que a torneira enche e assim o deposito nunca chegaria a estar cheio!
-
PedroSantos
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qua Dez 01, 2010 16:38
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: ensino secundário
- Andamento: cursando
 por Lorettto » Seg Dez 13, 2010 14:33
por Lorettto » Seg Dez 13, 2010 14:33
Obrigado....mas eu já tinha conseguido a resolução dele bem depois que postei aqui. Obrigado assim mesmo pela força, abraço !!

-
Lorettto
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Sáb Nov 27, 2010 01:17
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Uma Torneira Lança água em um tanque
por Chicharito » Sáb Dez 08, 2012 15:26
- 1 Respostas
- 2534 Exibições
- Última mensagem por Russman

Sáb Dez 08, 2012 15:36
Cálculo: Limites, Derivadas e Integrais
-
- [torneira em reservatório] ME AJUDA, É FACIL PARA VOCÊ
por leandro moraes » Sex Jun 03, 2011 13:04
- 2 Respostas
- 3356 Exibições
- Última mensagem por leandro moraes

Sex Jun 03, 2011 18:35
Cálculo: Limites, Derivadas e Integrais
-
- Problema
por fabio muniz » Qui Out 23, 2008 16:14
- 1 Respostas
- 10727 Exibições
- Última mensagem por admin

Ter Out 28, 2008 17:47
Problemas do Cotidiano
-
- Problema
por Lima » Dom Dez 14, 2008 18:08
- 3 Respostas
- 9738 Exibições
- Última mensagem por blangis

Dom Dez 14, 2008 20:15
Sistemas de Equações
-
- Problema..
por ANDRE RENATO PROFETA » Sex Mar 13, 2009 00:36
- 1 Respostas
- 3321 Exibições
- Última mensagem por Molina

Sex Mar 13, 2009 14:58
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



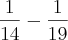
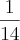 é maior que
é maior que 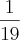 . Conclui-se que por cada unidade de tempo o depósito enche na diferença entre a torneira e a valvula.Seja n a quantidade de tempo.
. Conclui-se que por cada unidade de tempo o depósito enche na diferença entre a torneira e a valvula.Seja n a quantidade de tempo.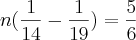



 .
.
 :
: