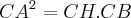por PedroSantos » Ter Dez 07, 2010 22:59
por PedroSantos » Ter Dez 07, 2010 22:59
Após alguma pesquisa encontrei uma forma de demonstrar algumas razões métricas de um triangulo retangulo.Nomeadamente:
-Cateto ao quadrado é igual ao produto da sua projecção sobre a hiputenusa pelo compromento da hipotenusa.

-O comprimento da altura relativa à hipotenusa ao quadrado é igual ao produto das projecções dos catetos sobre a hipotenusa.
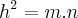
O método que encontrei, recorre à adição e ao produto escalar de vectores. Tomemos a seguinte figura:
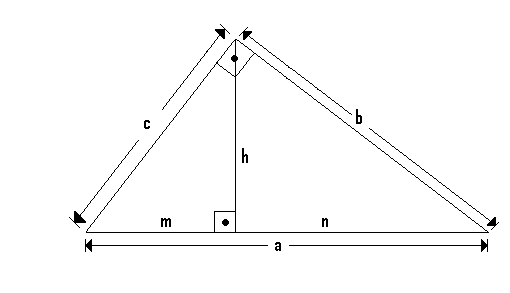
- triangulo1.png (3.01 KiB) Exibido 1768 vezes
Cada um dos vertices do triangulo têm uma identificação identica ao lado oposto e o pé da altura relativa à hipotenusa será denotado por H.
A primeira relação afirma que
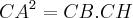
Então:
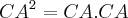
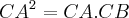
( a projecção da hipotenusa sobre um eixo ortognal é o cateto-base)
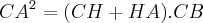
(decomposição de CA nos seus elementos)
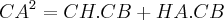
(os vectores HA e CB são prependiculares, o produto escalar é 0)
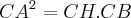
O vector CA corresponde ao cateto b, o CH corresponde à projecção de b sobre a hipotenusa e CB é o comprimento da hipotenusa.
Basta proceder de forma semelhante para a outra relação métrica.
Podem confirmar se o meu raciocino está correcto. Existem outras formas de demostrar estas relações métricas?
Fonte:
http://gilles.costantini.pagesperso-orange.fr/Lycee_fichiers/DevoirsP_fichiers/DM15.pdf
-
PedroSantos
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qua Dez 01, 2010 16:38
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: ensino secundário
- Andamento: cursando
 por VtinxD » Dom Dez 12, 2010 22:23
por VtinxD » Dom Dez 12, 2010 22:23
A forma que conheço para demonstra-las é através de semelhança entre os triângulos retângulos que aparecem na sua figura.
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Relaçoes metricas
 por DanielRJ » Dom Dez 18, 2011 13:22
por DanielRJ » Dom Dez 18, 2011 13:22
- 1 Respostas
- 1778 Exibições
- Última mensagem por DanielRJ

Dom Dez 18, 2011 15:33
Geometria Plana
-
- Relações Métricas
por janderson77 » Seg Dez 02, 2013 12:28
- 0 Respostas
- 943 Exibições
- Última mensagem por janderson77

Seg Dez 02, 2013 12:28
Geometria Plana
-
- relaçoes metricas nos triangulos
por stanley tiago » Sáb Fev 12, 2011 19:34
- 4 Respostas
- 2847 Exibições
- Última mensagem por stanley tiago

Dom Fev 13, 2011 18:04
Geometria Plana
-
- relaçoes metricas na circuferencia
 por stanley tiago » Seg Abr 11, 2011 18:37
por stanley tiago » Seg Abr 11, 2011 18:37
- 2 Respostas
- 2010 Exibições
- Última mensagem por stanley tiago

Ter Abr 12, 2011 10:06
Geometria Analítica
-
- Circunferencia e relações metricas
 por alfabeta » Qua Fev 29, 2012 00:09
por alfabeta » Qua Fev 29, 2012 00:09
- 0 Respostas
- 1692 Exibições
- Última mensagem por alfabeta

Qua Fev 29, 2012 00:09
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

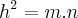
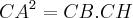
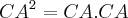
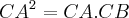 ( a projecção da hipotenusa sobre um eixo ortognal é o cateto-base)
( a projecção da hipotenusa sobre um eixo ortognal é o cateto-base)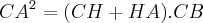 (decomposição de CA nos seus elementos)
(decomposição de CA nos seus elementos)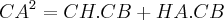 (os vectores HA e CB são prependiculares, o produto escalar é 0)
(os vectores HA e CB são prependiculares, o produto escalar é 0)