 por Samira » Sáb Nov 27, 2010 20:04
por Samira » Sáb Nov 27, 2010 20:04
Boa Noite pessoal!
O Problema é:

Solução: 2.
Substituindo o x por

cheguei a indeterminação

Depois de tentar as outras regras para resolver a indeterminação, usei a substituição de variável:

e ;

Quando

se Aproxima de

,

se aproxima de 0.
Ficou dessa forma:

E não consegui sair da indeterminação... Se alguém puder me dar uma dica, uma luz para prosseguir com o cálculo agradeceria muito mesmo!

-
Samira
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Nov 27, 2010 18:54
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Materiais (Polímeros)
- Andamento: cursando
 por Elcioschin » Sáb Nov 27, 2010 22:42
por Elcioschin » Sáb Nov 27, 2010 22:42
Vou tentar
Faça: a = x - pi/2 ----> x = a + pi/2 ----> x = (2a + pi)/2 ----> 2x = 2a + pi ----> x ----> pi/2 ----> a ---> 0
tg(2a + pi)/a = [sen(2a + pi)/cos(2a + pi)]/a = [(sen2a*cospi)/cos2a*cospi]/a = sen2a/a*cos2a = 2*sena*cosa/a*cos2a
tg(2a + pi)/a = (2*cosa/cos2a)*(sena/a)
Temos agora
Limite (sena/a) = 1 ----> Limite Fundamental
a-->0
Logo, o limite para a ---> 0 vale:
(2*1/1)*1 = 2
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Samira » Sáb Nov 27, 2010 23:49
por Samira » Sáb Nov 27, 2010 23:49
Consegui agora, faltava lembrar da identidade trigonométrica xD
O Problema é:
 Solução: 2.
Solução: 2.Substituindo o x por

cheguei a indeterminação

Substituição de variável:

e ;

Quando

se Aproxima de

,

se aproxima de 0.

Aplicando a identidade trigonométrica...


Então,


e ai ficou


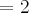
Obrigada Elcioschin

-
Samira
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Nov 27, 2010 18:54
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Materiais (Polímeros)
- Andamento: cursando
 por andrefahl » Dom Nov 28, 2010 00:06
por andrefahl » Dom Nov 28, 2010 00:06
Bom só pra lembrar tb,
quando se tem indeterminações do tipo 0/0 ou infinito sobre infinito
pode-se usar a regra de L'Hospitall =)
deriva em cima e embaixo ateh se livrar da indeterminação =)
pode ser q de menos trabalho!
-
andrefahl
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Qui Out 28, 2010 18:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física - UNICAMP
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Indeterminação - Limite
por Paloma » Ter Mar 16, 2010 21:06
- 10 Respostas
- 9739 Exibições
- Última mensagem por Paloma

Sáb Mar 20, 2010 13:57
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Indeterminação
 por Aliocha Karamazov » Sex Nov 25, 2011 00:28
por Aliocha Karamazov » Sex Nov 25, 2011 00:28
- 2 Respostas
- 1956 Exibições
- Última mensagem por Aliocha Karamazov

Sex Nov 25, 2011 21:21
Cálculo: Limites, Derivadas e Integrais
-
- Limite indeterminação 0/0
por ravi » Ter Mai 08, 2012 06:42
- 1 Respostas
- 1388 Exibições
- Última mensagem por LuizAquino

Ter Mai 08, 2012 12:13
Cálculo: Limites, Derivadas e Integrais
-
- [Limite no infinito]casos de indeterminação
por moyses » Sex Set 09, 2011 00:24
- 9 Respostas
- 5680 Exibições
- Última mensagem por LuizAquino

Seg Set 12, 2011 12:18
Cálculo: Limites, Derivadas e Integrais
-
- [Calculo de limite] quando há indeterminação 0/0
por JessicaDias » Qui Abr 12, 2012 20:00
- 2 Respostas
- 3004 Exibições
- Última mensagem por JessicaDias

Qui Abr 12, 2012 21:35
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 cheguei a indeterminação
cheguei a indeterminação 
 e ;
e ; 
 se Aproxima de
se Aproxima de  ,
,  se aproxima de 0.
se aproxima de 0.







 e ai ficou
e ai ficou 

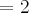

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.