Problema probabilidade MEGASENA!

[camilesfnogueira]

Boa noite, pessoal!
Precisava resolver um problema sobre a Megasena, entretanto estou estudando sobre o assunto, mas não saio do lugar...não estou conseguindo resolver..
Tenho uma lista do excel com os números que mais saíram e os que menos saíram em CADA DEZENA das 6 sorteadas na MEGASENA

Números que menos saíram :
1ª DEZENA
18 => 9 vezes

2ª DEZENA
29 e 38 => 13 vezes cada um

3ª DEZENA
26=> 11 vezes

4ª DEZENA
22=> 12 vezes

5ª DEZENA
26 e 27=> 12 vezes cada um

6ª DEZENA
11=> 12 vezes

Números que mais saíram

1ª DEZENA
49 => 31 vezes

2ª DEZENA
5 e 17 => 31 vezes cada um

3ª DEZENA
4=> 31 vezes

4ª DEZENA
29=> 32 vezes

5ª DEZENA
44=> 31 vezes cada um

6ª DEZENA
23 e 33=> 29 vezes


Esses números foram retirados de 1220 jogos. Com base nisto, preciso descobrir a probabilidade de sair a sequência com os números menos sorteados neste 1220 concursos. E depois fazer o mesmo com os números mais sorteados, ou seja, a probabilidade de sair a sequência com os números mais sorteados nesses 1220 concursos.

Pensei na a quantidade de vezes que saiu cada um e dividi pelo total (1220) e peguei isto e multipliquei pela chance de um número qualquer sair em cada dezena; na 2a dezena, por exemplo, 2/59.

Mostrando em números a probabilidade da sequencia formada pelos números que menos saíram: 18 => 9 vezes, 29 e 38 => 13 vezes cada (26 total), 26=> 11 vezes, 22=> 12 vezes, 27=> 12 vezes, 11=> 12 vezes

1/60 x 9/1220 + 2/59 x 26/1220 + 1/58 x 11/1220+ 1/57 x 12/1220 + 1/56 x 12/1220 + 1/55 x 12/1220

A 5ª dezena (amarelo) eu excluí o 26, pois ele, obrigatoriamente sairia na 3ª dezena, diferentemente da 2a dezena em que considerei os 2 números que menos saíram.

Foi isso que pensei...alguem pode me ajudar? Acho que não é tão simples assim.

[alexandre32100]

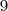A probabilidade de sair o número é de 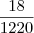, por exemplo. A probabilidade que você procura deve ser 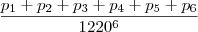, onde cada um dos p's é igual a quantas vezes o número que você escolheu caiu. Espero ter ajudado.

[camilesfnogueira]

Acho que até seria assim, se não importassem as dezenas, mas neste problema em si, a avaliação é feita sobre cada uma das 6 dezenas. O número 18 saiu 9 vezes na primeira dezena e na 1a dezena como ainda constam todas os números (60) a probabilidade é menor, mas já na segunda dezena por exemplo, se o número 18 tivesse saído 9 vezes também, sua probabilidade seria influenciada pelo fato que uma bola ja foi eliminada na 1a dezena, ou seja, é menos um número pra concorrer no sorteio, já que a bola que saiu na 1a dezena fica de fora.
Brigada pela ajuda..ainda continuo pensando =)
Qualquer ajuda será bem vinda!