Essa é uma série do OBJETIVO, alguns não consegui resolver, help ..!
(fuvest) - De um poligono convexo P de n lados, calcular o número de poligonos convexos, cujos vértices são vértices de P.
UFMG - O Risco de contrair-se uma determinada doença é proporcional à razão entre o número de pessoas infectadas por essa doença e a população da cidade, nessa ordem. Numa cidade A de 40000 habitantes com 660 infectadas, o risco de contrair-se essa doença é 0,06.
Numa cidade que tem 2% de sua população infectada e em que a constante de proporcionalidade é igual à da cidade A, o risco de contrair-se essa doença é:
(FUVEST) Num torneio de tênis, no qual todas as partidas são eliminatórias, estão inscritos 8 jogadores. Para definir-se a primeira rodada do torneio, realiza-se um sorteio casual que divide os 8 jogadores em 4 grupos de 2 jogadores cada um.
a) No torneio estão inscritos quatro amigos A, B, C e D. Nenhum deles gostaria de enfrentar um dos outros logo na primeira rodada do torneio. Qual a probabilidade de que esse desejo seja satisfeito?
b) Sabendo-se que pelo menos um dos jogos da primeira rodada envolve 2dos 4 amigos, qual a probabilidade condicional de que A e B se enfrentam na primeira rodada?
quem puder ajudar, muito obrigado!


 lados (triângulos). Devemos escolher
lados (triângulos). Devemos escolher  . Isto pode ser feito de
. Isto pode ser feito de  maneiras. Este mesmo raciocínio vale para qualquer inteiro
maneiras. Este mesmo raciocínio vale para qualquer inteiro  com
com 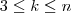 .
.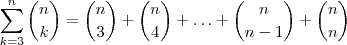 .
.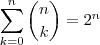 . Portanto,
. Portanto, 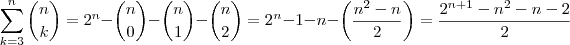 (se é que isto ajuda em algum ponto
(se é que isto ajuda em algum ponto  )
) .
.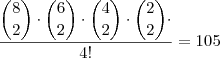 .
.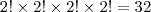 .
.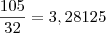 ou
ou 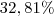 .
.
 .
.
 :
: