Estou com dúvida na seguinte questão:
(UF.GO) O conjunto-solução da inequação
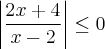 é:
é:a) {x ? ? : x = -2}
b) {x ? ? : x ? 2}
c) {x ? ? : x = 2}
d) {x ? ? : -2< x ?2}
e) {x ? ? : x< -2 ou x >2}
Resolvi assim:
2x+4 ? 0
2x+4 =0
2x=-4

x=-2
x-2 < 0
x-2 = 0
x=2

Estudo dos snais:

S={x ? ? : -2? x <2}
Mas a resposta do gabarito é letra A, alguém poderia me explicar como chegar neste resultado?


 tem-se
tem-se  .
.  = conjunto dos números reais
= conjunto dos números reais 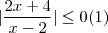 .
. 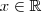 , então
, então 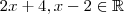 e portanto
e portanto 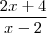 também é um número real o que nos garanti que
também é um número real o que nos garanti que 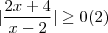 .
.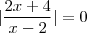 .
.
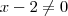 (Caso contrário teríamos indeterminação ) .
(Caso contrário teríamos indeterminação ) . 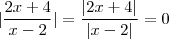 o que implica que
o que implica que 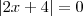 o que implica que
o que implica que 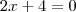 ...
...
 .
.
 :
: