Ajuda em exercício

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

Ajuda em exercício

Regras do fórum
Responder

Ajuda em exercício

Mensagempor Lola » Qua Mai 08, 2013 14:50

Olá,
Alguém por favor poderia me ajudar a resolver esse exercício?

Encontre o conjunto solução de:

?(x²-4x+5) > 2

PS: x²-4x+5 está dentro da raiz quadrada.

Eu achei a solução como sendo x> 2?3 e x <-2?3, é isso mesmo??? :$

Obrigada!!!
Lola
Usuário Ativo
Usuário Ativo
 
Mensagens: 11
Registrado em: Sex Mar 18, 2011 18:31
Localização: São Paulo
Formação Escolar: ENSINO MÉDIO
Andamento: cursando
Voltar ao topo

Re: Ajuda em exercício

Mensagempor brunoiria » Qua Mai 08, 2013 22:44

Bom Lola, seu problema é este
\sqrt{x^2-4x+5}>2
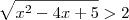
Assim, vc terá que elevar ambos os lados da equação ao quadrado.
(\sqrt{x^2-4x+5})^2>2^2\Rightarrow x^2-4x+5>4\Rightarrow x^2-4x+1>0
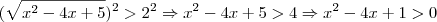
Assim resolvendo a equação, vc achará a solução.
Espero ter ajudado....
brunoiria
Usuário Ativo
Usuário Ativo
 
Mensagens: 11
Registrado em: Sáb Jun 23, 2012 10:32
Formação Escolar: GRADUAÇÃO
Área/Curso: Lic Mat
Andamento: cursando
Voltar ao topo
Responder

Voltar para Inequações

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 


Tópico Popular

Assunto: Conjunto dos números racionais.
Autor: scggomes - Sex Fev 18, 2011 10:38

Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:

Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?

Grata.

Assunto: Conjunto dos números racionais.
Autor: MarceloFantini - Sex Fev 18, 2011 12:27

x^2 = \frac{x}{3}

Assunto: Conjunto dos números racionais.
Autor: scggomes - Sex Fev 18, 2011 12:55

também pensei que fosse assim, mas a resposta é \frac{1}{3}.

Obrigada Fantini.

Assunto: Conjunto dos números racionais.
Autor: MarceloFantini - Sex Fev 18, 2011 13:01

x^2 = \frac{x}{3} \Rightarrow x^2 - \frac{x}{3} = 0 \Rightarrow x \left(x - \frac{1}{3} \right) = 0

Como x \neq 0:

x - \frac{1}{3} = 0 \Rightarrow x = \frac{1}{3}

O que você fez?

Assunto: Conjunto dos números racionais.
Autor: scggomes - Sex Fev 18, 2011 16:17

eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.

Obrigada.

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum