 [/tex]
[/tex]Eu tenho a resposta deste exercício, mas gostaria que me ajudassem a melhor compreendê-la:
Resposta: Por hipótese ax = a e como
![[tex]a\neq0\, existe\, {a}^{-1} [tex]a\neq0\, existe\, {a}^{-1}](/latexrender/pictures/05c7ab4f181a5899e9c414da307aa9b4.png)
![Logo[tex]\, {a}^{-1}(ax) = x\, Logo[tex]\, {a}^{-1}(ax) = x\,](/latexrender/pictures/8094995f56eb71fd86f4c4dbf35667e9.png) por um lado[/tex]
por um lado[/tex]e por outro
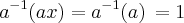 por outro.
por outro.
\,Não saberia reproduzir a resolução se me deparasse com este exercício
no futuro... Eu sei que é usada a propriedade de dado um número
 ,este número possui inverso
,este número possui inverso![[tex] \,{a}^{-1} \,tal\, que \,a . {a}^{-1} = 1\, [tex] \,{a}^{-1} \,tal\, que \,a . {a}^{-1} = 1\,](/latexrender/pictures/cf722ec9b201ea0155c37f2d2ac9e191.png) [/tex]
[/tex]Mas este começo
![[tex]\, {a}^{-1} (ax)= x\, [tex]\, {a}^{-1} (ax)= x\,](/latexrender/pictures/13a20abc628fe202b2576882e055de6d.png) [/tex] me parece confuso...
[/tex] me parece confuso...

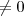 ,existe um único real
,existe um único real  tal que
tal que  .Tal
.Tal  ,
,  .
.  ou seja
ou seja  .
.
 ?
?  (Existência de elemento neutro )
(Existência de elemento neutro )  (Existência de inverso )
(Existência de inverso )  (Associativa )
(Associativa ) ???
??? ???
??? ???
??? .
.  .
. .
.