 por bebelo32 » Sex Mar 18, 2016 17:16
por bebelo32 » Sex Mar 18, 2016 17:16
1) Verificar quais são espaço vetoriais. para aqueles que não são,citar os axiomas que não se verificam
a) {(x,2x,3x); x ? ?} com as operações usuais
b) ?² com as operações: (a,b)+(c,d) = (a,b) ? (a,b) = (?a,?b)
c) A = {(x,y) ? ?²/ y = 5x} com as operações usuais
d) ?², com as operações: (x,y) + (x',y') = (x+x',y+y') ? (x,y) = (? x,0)
a letra A e C sao espaço vetoriais pq e B e D nao sao espaço vetoriais pq
-
bebelo32
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Sáb Mai 03, 2014 19:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: computação
- Andamento: formado
 por adauto martins » Qua Mar 23, 2016 15:58
por adauto martins » Qua Mar 23, 2016 15:58
no q. pude entender esse

seria o operador multiplicativo ou seja:
seja
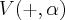
um espaço vetorial sobre um corpo

b)
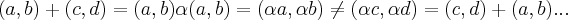
p/
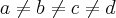
,ou seja nao ha comutatividade de somas e produtos...
d)o mesmo raciocinio do anterior,resolva-o...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por 0 kelvin » Qua Mar 23, 2016 16:15
por 0 kelvin » Qua Mar 23, 2016 16:15
Esses exercícios de subespaço vetorial onde são dadas operações "estranhas" se resolvem usando essa operação dada. Vc deve ter visto os axiomas, aplique a propriedade da multiplicação por escalar, do elemento nulo e da soma no conjunto dado. Só que no lugar de multiplicar e somar como se faz normalmente, multiplique e some do jeito que esta dado naquele conjunto.
-
0 kelvin
- Usuário Parceiro

-
- Mensagens: 78
- Registrado em: Dom Out 31, 2010 16:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias atmosfericas
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Algebra Linear] - Matriz de uma trasnformacao linear, Ajuda
por rodrigojuara » Dom Nov 30, 2014 15:05
- 1 Respostas
- 8154 Exibições
- Última mensagem por adauto martins

Seg Dez 01, 2014 16:12
Álgebra Linear
-
- [Algebra Linear] - Composição de transformação Linear
por aligames321 » Ter Dez 04, 2012 23:53
- 1 Respostas
- 10528 Exibições
- Última mensagem por young_jedi

Qua Dez 05, 2012 12:45
Álgebra Linear
-
- Álgebra Linear -Transformação linear- Isomorfismo
por anapaulasql » Ter Jan 27, 2015 22:08
- 1 Respostas
- 11560 Exibições
- Última mensagem por adauto martins

Ter Mar 29, 2016 13:15
Álgebra Linear
-
- [Álgebra Linear] Transformação Linear Idenpotente
por Zubumafu67 » Ter Nov 17, 2020 11:38
- 0 Respostas
- 13601 Exibições
- Última mensagem por Zubumafu67

Ter Nov 17, 2020 11:38
Álgebra Linear
-
- [Álgebra Linear] Transformação linear
por Debby » Dom Mai 27, 2012 12:17
- 2 Respostas
- 9140 Exibições
- Última mensagem por Debby

Dom Mai 27, 2012 20:27
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 seria o operador multiplicativo ou seja:
seria o operador multiplicativo ou seja: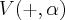 um espaço vetorial sobre um corpo
um espaço vetorial sobre um corpo 
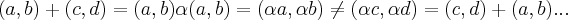 p/
p/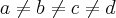 ,ou seja nao ha comutatividade de somas e produtos...
,ou seja nao ha comutatividade de somas e produtos...
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
