Determinar a projeção ortogonal do vetor
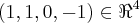 sobre o subespaço
sobre o subespaço 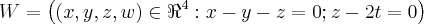 .
.Precisamos, primeiro, encontrar a base ortonormal de W. Consegui encontrar através do Processo de Gram-Schmidt:
![B = \left(\left( \frac{2}{3}(1, 0, 1, \frac{1}{2}) \right), \left(\frac{3}{\sqrt[]{14}}\left(5, 9, -4, -2 \right) \right) \right) B = \left(\left( \frac{2}{3}(1, 0, 1, \frac{1}{2}) \right), \left(\frac{3}{\sqrt[]{14}}\left(5, 9, -4, -2 \right) \right) \right)](/latexrender/pictures/7bc409928552b8e1e918e1fdda1e3ce5.png) . Contudo, ao aplicar
. Contudo, ao aplicar 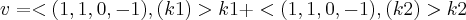 , onde v é a projeção procurada e, k1 e k2 são os vetores da base ortonormal, simplesmente não dá certo! Eu não sei o que há de errado! Por favor, preciso de ajuda!!!!
, onde v é a projeção procurada e, k1 e k2 são os vetores da base ortonormal, simplesmente não dá certo! Eu não sei o que há de errado! Por favor, preciso de ajuda!!!!Muito Obrigada!


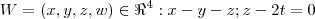
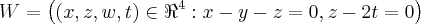 , mas que também está estranho....
, mas que também está estranho....
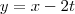
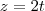
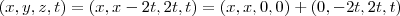
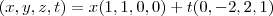
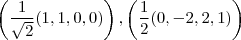
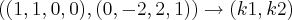 a base ortonormal;
a base ortonormal;![k1 = \frac{(1,1,0,0)}{\sqrt[]{<(1,1,0,0),(1,1,0,0)>}} k1 = \frac{(1,1,0,0)}{\sqrt[]{<(1,1,0,0),(1,1,0,0)>}}](/latexrender/pictures/9d5da7625d24be8e8f4fd0698eb993aa.png)
![= \frac{(1,1,0,0)}{\sqrt[]{2}} = \frac{1}{\sqrt[]{2}}(1,1,0,0) = \frac{(1,1,0,0)}{\sqrt[]{2}} = \frac{1}{\sqrt[]{2}}(1,1,0,0)](/latexrender/pictures/fcd574e7619847af0cbc791e458fd666.png)
![k2 = \frac{(0,-2,2,1) - <(0,-2,2,1),(\frac{1}{\sqrt[]{2}}(1,1,0,0)>\frac{1}{\sqrt[]{2}}(1,1,0,0)}{||(0,-2,2,1) - <(0,-2,2,1),(\frac{1}{\sqrt[]{2}}(1,1,0,0)>\frac{1}{\sqrt[]{2}}(1,1,0,0)||} k2 = \frac{(0,-2,2,1) - <(0,-2,2,1),(\frac{1}{\sqrt[]{2}}(1,1,0,0)>\frac{1}{\sqrt[]{2}}(1,1,0,0)}{||(0,-2,2,1) - <(0,-2,2,1),(\frac{1}{\sqrt[]{2}}(1,1,0,0)>\frac{1}{\sqrt[]{2}}(1,1,0,0)||}](/latexrender/pictures/27753769d12cf0349883dd3d4e670f9b.png) =
= ![\frac{(0,-2,2,1)+(1,1,0,0)}{||(0,-2,2,1)+(1,1,0,0)||} = \frac{(1,-1,2,1)}{\sqrt[]{7}} \frac{(0,-2,2,1)+(1,1,0,0)}{||(0,-2,2,1)+(1,1,0,0)||} = \frac{(1,-1,2,1)}{\sqrt[]{7}}](/latexrender/pictures/ae4de1872709f462daef564b569d12ca.png)
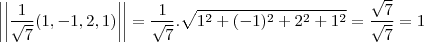

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)