 por Pessoa Estranha » Seg Set 08, 2014 18:54
por Pessoa Estranha » Seg Set 08, 2014 18:54
Boa tarde, pessoal! Preciso de ajuda!
Determinar a projeção ortogonal do vetor
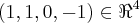
sobre o subespaço
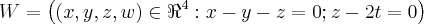
.
Precisamos, primeiro, encontrar a base ortonormal de W. Consegui encontrar através do Processo de Gram-Schmidt:
![B = \left(\left( \frac{2}{3}(1, 0, 1, \frac{1}{2}) \right), \left(\frac{3}{\sqrt[]{14}}\left(5, 9, -4, -2 \right) \right) \right) B = \left(\left( \frac{2}{3}(1, 0, 1, \frac{1}{2}) \right), \left(\frac{3}{\sqrt[]{14}}\left(5, 9, -4, -2 \right) \right) \right)](/latexrender/pictures/7bc409928552b8e1e918e1fdda1e3ce5.png)
. Contudo, ao aplicar
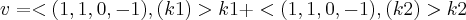
, onde v é a projeção procurada e, k1 e k2 são os vetores da base ortonormal, simplesmente não dá certo! Eu não sei o que há de errado! Por favor, preciso de ajuda!!!!
Muito Obrigada!
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por young_jedi » Qui Set 11, 2014 11:14
por young_jedi » Qui Set 11, 2014 11:14
no enunciado você tem
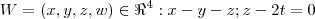
tem certeza que é t na equação e não w ou vice e versa ?
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Pessoa Estranha » Sex Set 12, 2014 19:16
por Pessoa Estranha » Sex Set 12, 2014 19:16
Obrigada por responder!
Olha, estou verificando aqui o enunciado e, realmente, eu errei na hora de digitar. O que está escrito é:
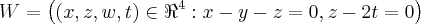
, mas que também está estranho....
Mesmo assim, obrigada!

-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por young_jedi » Dom Set 14, 2014 11:55
por young_jedi » Dom Set 14, 2014 11:55
nesse caso você pode fixar as variaveis x e t e fazer
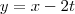
e
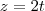
portanto
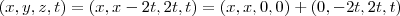
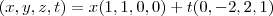
dividindo esses vetores por seus modulos para termos os vetores unitários teríamos a base ortonormal
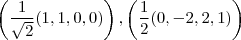
agora é só aplicar o procedimento que você estava utilizando
qualquer duvida comente
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Pessoa Estranha » Dom Set 14, 2014 12:31
por Pessoa Estranha » Dom Set 14, 2014 12:31
Bom, então, pelo processo de Gram-Schmidt, temos:
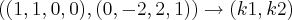
a base ortonormal;
![k1 = \frac{(1,1,0,0)}{\sqrt[]{<(1,1,0,0),(1,1,0,0)>}} k1 = \frac{(1,1,0,0)}{\sqrt[]{<(1,1,0,0),(1,1,0,0)>}}](/latexrender/pictures/9d5da7625d24be8e8f4fd0698eb993aa.png)
![= \frac{(1,1,0,0)}{\sqrt[]{2}} = \frac{1}{\sqrt[]{2}}(1,1,0,0) = \frac{(1,1,0,0)}{\sqrt[]{2}} = \frac{1}{\sqrt[]{2}}(1,1,0,0)](/latexrender/pictures/fcd574e7619847af0cbc791e458fd666.png)
![k2 = \frac{(0,-2,2,1) - <(0,-2,2,1),(\frac{1}{\sqrt[]{2}}(1,1,0,0)>\frac{1}{\sqrt[]{2}}(1,1,0,0)}{||(0,-2,2,1) - <(0,-2,2,1),(\frac{1}{\sqrt[]{2}}(1,1,0,0)>\frac{1}{\sqrt[]{2}}(1,1,0,0)||} k2 = \frac{(0,-2,2,1) - <(0,-2,2,1),(\frac{1}{\sqrt[]{2}}(1,1,0,0)>\frac{1}{\sqrt[]{2}}(1,1,0,0)}{||(0,-2,2,1) - <(0,-2,2,1),(\frac{1}{\sqrt[]{2}}(1,1,0,0)>\frac{1}{\sqrt[]{2}}(1,1,0,0)||}](/latexrender/pictures/27753769d12cf0349883dd3d4e670f9b.png)
=
![\frac{(0,-2,2,1)+(1,1,0,0)}{||(0,-2,2,1)+(1,1,0,0)||} = \frac{(1,-1,2,1)}{\sqrt[]{7}} \frac{(0,-2,2,1)+(1,1,0,0)}{||(0,-2,2,1)+(1,1,0,0)||} = \frac{(1,-1,2,1)}{\sqrt[]{7}}](/latexrender/pictures/ae4de1872709f462daef564b569d12ca.png)
o k2 não está unitário...
não estou conseguindo achar o meu erro...
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por young_jedi » Dom Set 14, 2014 15:20
por young_jedi » Dom Set 14, 2014 15:20
no meu ver esta correto o k2 é isto mesmo e ele é unitario sim
se você tirar seu modulo você vera que é igual a 1
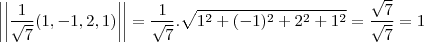
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Pessoa Estranha » Dom Set 14, 2014 16:16
por Pessoa Estranha » Dom Set 14, 2014 16:16
Ah! Tem razão!

Muito Obrigada!
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Álgebra Linear] Socorro!
por Pessoa Estranha » Seg Set 08, 2014 18:25
- 0 Respostas
- 1427 Exibições
- Última mensagem por Pessoa Estranha

Seg Set 08, 2014 18:25
Álgebra Linear
-
- [Algebra Linear] - Matriz de uma trasnformacao linear, Ajuda
por rodrigojuara » Dom Nov 30, 2014 15:05
- 1 Respostas
- 8159 Exibições
- Última mensagem por adauto martins

Seg Dez 01, 2014 16:12
Álgebra Linear
-
- [Algebra Linear] - Composição de transformação Linear
por aligames321 » Ter Dez 04, 2012 23:53
- 1 Respostas
- 10532 Exibições
- Última mensagem por young_jedi

Qua Dez 05, 2012 12:45
Álgebra Linear
-
- Álgebra Linear -Transformação linear- Isomorfismo
por anapaulasql » Ter Jan 27, 2015 22:08
- 1 Respostas
- 11565 Exibições
- Última mensagem por adauto martins

Ter Mar 29, 2016 13:15
Álgebra Linear
-
- [Álgebra Linear] Transformação Linear Idenpotente
por Zubumafu67 » Ter Nov 17, 2020 11:38
- 0 Respostas
- 13607 Exibições
- Última mensagem por Zubumafu67

Ter Nov 17, 2020 11:38
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
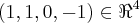 sobre o subespaço
sobre o subespaço 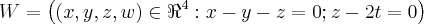 .
.![B = \left(\left( \frac{2}{3}(1, 0, 1, \frac{1}{2}) \right), \left(\frac{3}{\sqrt[]{14}}\left(5, 9, -4, -2 \right) \right) \right) B = \left(\left( \frac{2}{3}(1, 0, 1, \frac{1}{2}) \right), \left(\frac{3}{\sqrt[]{14}}\left(5, 9, -4, -2 \right) \right) \right)](/latexrender/pictures/7bc409928552b8e1e918e1fdda1e3ce5.png) . Contudo, ao aplicar
. Contudo, ao aplicar 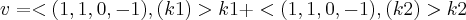 , onde v é a projeção procurada e, k1 e k2 são os vetores da base ortonormal, simplesmente não dá certo! Eu não sei o que há de errado! Por favor, preciso de ajuda!!!!
, onde v é a projeção procurada e, k1 e k2 são os vetores da base ortonormal, simplesmente não dá certo! Eu não sei o que há de errado! Por favor, preciso de ajuda!!!!

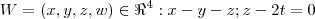
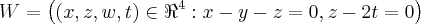 , mas que também está estranho....
, mas que também está estranho....
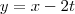
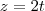
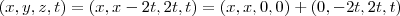
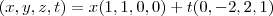
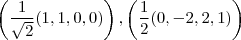
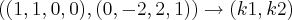 a base ortonormal;
a base ortonormal;![k1 = \frac{(1,1,0,0)}{\sqrt[]{<(1,1,0,0),(1,1,0,0)>}} k1 = \frac{(1,1,0,0)}{\sqrt[]{<(1,1,0,0),(1,1,0,0)>}}](/latexrender/pictures/9d5da7625d24be8e8f4fd0698eb993aa.png)
![= \frac{(1,1,0,0)}{\sqrt[]{2}} = \frac{1}{\sqrt[]{2}}(1,1,0,0) = \frac{(1,1,0,0)}{\sqrt[]{2}} = \frac{1}{\sqrt[]{2}}(1,1,0,0)](/latexrender/pictures/fcd574e7619847af0cbc791e458fd666.png)
![k2 = \frac{(0,-2,2,1) - <(0,-2,2,1),(\frac{1}{\sqrt[]{2}}(1,1,0,0)>\frac{1}{\sqrt[]{2}}(1,1,0,0)}{||(0,-2,2,1) - <(0,-2,2,1),(\frac{1}{\sqrt[]{2}}(1,1,0,0)>\frac{1}{\sqrt[]{2}}(1,1,0,0)||} k2 = \frac{(0,-2,2,1) - <(0,-2,2,1),(\frac{1}{\sqrt[]{2}}(1,1,0,0)>\frac{1}{\sqrt[]{2}}(1,1,0,0)}{||(0,-2,2,1) - <(0,-2,2,1),(\frac{1}{\sqrt[]{2}}(1,1,0,0)>\frac{1}{\sqrt[]{2}}(1,1,0,0)||}](/latexrender/pictures/27753769d12cf0349883dd3d4e670f9b.png) =
= ![\frac{(0,-2,2,1)+(1,1,0,0)}{||(0,-2,2,1)+(1,1,0,0)||} = \frac{(1,-1,2,1)}{\sqrt[]{7}} \frac{(0,-2,2,1)+(1,1,0,0)}{||(0,-2,2,1)+(1,1,0,0)||} = \frac{(1,-1,2,1)}{\sqrt[]{7}}](/latexrender/pictures/ae4de1872709f462daef564b569d12ca.png)
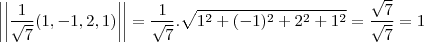


 .
.



