 Não estou conseguindo resolver este exercício:
Não estou conseguindo resolver este exercício:Considere os vetores: {(1,1,2),(2,-1,4),(2,4,4)}. Encontre um vetor norma 1 ortogonal aos 3 vetores dados e então, determine módulo da soma de suas entradas.
Gabarito:
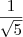
Por favor, se alguém puder me ajudar, mesmo que uma sugestão, ficarei grato.





 (porque no enunciado diz que a norma é igual a 1), substituindo x e y pela escrita deles em função de
(porque no enunciado diz que a norma é igual a 1), substituindo x e y pela escrita deles em função de  .
. e
e  .
.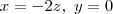 e
e 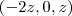 .
.
 , podes escrever que:
, podes escrever que: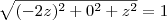
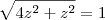
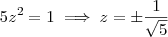
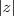 , esta soma será igual a
, esta soma será igual a 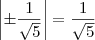
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)