V1 = (4, 2, -3)
V2 = (2, 1, -2)
V3 = (-2, -1, 0)
Olá, me deparei com esse exercício na minha apostila de gaal, porém não estou conseguindo resolver. Fiz a matriz com esses vetores e achei como solução {
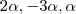 }, assim sendo, a base seria o vetor (2,-3, 1) e a dimensão seria 1, creio eu.
}, assim sendo, a base seria o vetor (2,-3, 1) e a dimensão seria 1, creio eu.Mas no livro a dimensão do subespaço aparece como 2.
Alguém me explica no que estou errando, por favor?
Muito Grato


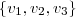 é linearmente independente. Você verificou isso? Se sim, não há mais o que fazer. Se não, quantos sobram?
é linearmente independente. Você verificou isso? Se sim, não há mais o que fazer. Se não, quantos sobram?

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)