 por Carlos Robert » Qua Nov 09, 2011 09:03
por Carlos Robert » Qua Nov 09, 2011 09:03
A resolucao do seguinte exercício:
Resolve-se fazer uma aplicacao a juros compostos hoje,para daqui a 8 meses retire R$ 1500,00
e R$ 3500,00 ao fim de um ano.Quanto deve-se investir então hoje, sabendo que o banco oferece uma taxa de 10%ao ano?
A resolução seria por meio da expressão?
V= 1500,00/(1+0,10)8+ 3500,00/(1+0,10)12
Como resolvê-la?
obrigado
-
Carlos Robert
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Nov 08, 2011 21:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Contábeis
- Andamento: cursando
 por MarceloFantini » Qua Nov 09, 2011 21:39
por MarceloFantini » Qua Nov 09, 2011 21:39
Seja

a taxa ao
mês. Sabemos que

pelo enunciado. Seja
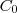
a quantidade inicial de dinheiro. Sabemos que após 8 meses, ele se tornará
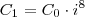
. Daí, retiramos 1500 reais. Passados mais quatro meses, completando um ano, retiramos os 3500 faltantes, logo:
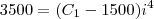
. Substituindo a primeira na segunda, teremos
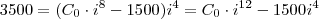
, de onde concluímos que
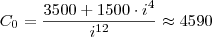
reais.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Juros Simples // Juros Compostos
por Roberta » Qui Jul 16, 2009 18:22
- 3 Respostas
- 8222 Exibições
- Última mensagem por Roberta

Qui Jul 16, 2009 19:46
Matemática Financeira
-
- juros compostos
por pseytow » Seg Jul 07, 2008 23:03
- 1 Respostas
- 5476 Exibições
- Última mensagem por Molina

Seg Jul 07, 2008 23:55
Matemática Financeira
-
- Juros compostos
por Vanessa » Ter Set 16, 2008 12:28
- 2 Respostas
- 4044 Exibições
- Última mensagem por Vanessa

Ter Out 28, 2008 17:22
Matemática Financeira
-
- JUROS COMPOSTOS
por Gir » Seg Set 14, 2009 11:24
- 19 Respostas
- 28479 Exibições
- Última mensagem por rodrigoadmgp

Seg Jan 25, 2010 21:11
Matemática Financeira
-
- Juros Compostos
por Danilo Dias Vilela » Qui Out 15, 2009 12:37
- 1 Respostas
- 2464 Exibições
- Última mensagem por carlos r m oliveira

Sex Out 16, 2009 11:43
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 a taxa ao
a taxa ao  pelo enunciado. Seja
pelo enunciado. Seja 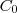 a quantidade inicial de dinheiro. Sabemos que após 8 meses, ele se tornará
a quantidade inicial de dinheiro. Sabemos que após 8 meses, ele se tornará 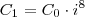 . Daí, retiramos 1500 reais. Passados mais quatro meses, completando um ano, retiramos os 3500 faltantes, logo:
. Daí, retiramos 1500 reais. Passados mais quatro meses, completando um ano, retiramos os 3500 faltantes, logo: 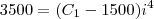 . Substituindo a primeira na segunda, teremos
. Substituindo a primeira na segunda, teremos 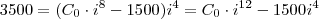 , de onde concluímos que
, de onde concluímos que 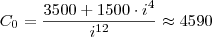 reais.
reais.


 .
.



