 por grilo » Dom Set 30, 2012 13:20
por grilo » Dom Set 30, 2012 13:20
Se alguém puder me ajudar, to com dificuldade nesse exercício.
Verifique que a derivação e a integração comutam, se são calculadas sobre variáveis distintas, ou seja, d/dx(
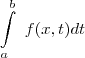
)=
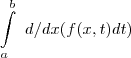
.
Pensei em fazer com um exemplo, mas preciso de um modo que prove que pra qualquer função do tipo isso aconteça, acho que utilizando a definição de integral pode resolver, mas não sei como aplicar.
Editado pela última vez por
grilo em Dom Set 30, 2012 20:22, em um total de 2 vezes.
-
grilo
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Nov 01, 2010 19:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Dom Set 30, 2012 13:47
por MarceloFantini » Dom Set 30, 2012 13:47
Prezado
Grilo,
Por favor, antes de postar um tópico leia as
Regras deste Fórum. Em especial, vide as regras 1 e 2.
O seu tópico não deverá ser respondido antes de estar de acordo com as regras.
Atenciosamente,
Equipe de ModeradoresFuturo MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função Gama.
por 380625 » Sáb Jun 01, 2013 16:57
- 1 Respostas
- 948 Exibições
- Última mensagem por e8group

Dom Jun 02, 2013 20:04
Cálculo: Limites, Derivadas e Integrais
-
- Função real definida pela soma de uma função par c/uma ímpar
por Taah » Sáb Mar 27, 2010 15:33
- 3 Respostas
- 5578 Exibições
- Última mensagem por Taah

Dom Mar 28, 2010 13:21
Funções
-
- [plano tangente a função de duas variaveis dada por função]
por isaac naruto » Qui Dez 31, 2015 16:35
- 0 Respostas
- 4592 Exibições
- Última mensagem por isaac naruto

Qui Dez 31, 2015 16:35
Cálculo: Limites, Derivadas e Integrais
-
- [Desigualdade] entre função exponencial e função potência
por VitorFN » Sex Mai 26, 2017 15:18
- 1 Respostas
- 5751 Exibições
- Última mensagem por adauto martins

Sex Jul 07, 2017 12:17
Álgebra Elementar
-
- +uma função das trevas.ajuda aew!(função par mas heim!?)
por Fabricio dalla » Dom Fev 27, 2011 16:12
- 2 Respostas
- 3489 Exibições
- Última mensagem por LuizAquino

Dom Mar 06, 2011 09:17
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
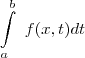 )=
)=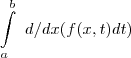 .
. 


