 por FelipeTURBO » Qui Jun 14, 2012 14:15
por FelipeTURBO » Qui Jun 14, 2012 14:15
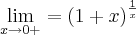
A resposta desse exercício seria
'e'. Como consigo chegar nessa resposta, já fiz de uma maneira porem a professora disse estar errado.
-
FelipeTURBO
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Mar 23, 2012 23:08
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por joaofonseca » Qui Jun 14, 2012 14:46
por joaofonseca » Qui Jun 14, 2012 14:46
Seja,
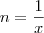
. Então
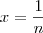
Assim, quando
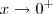
,
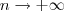
.
Podemos escrever:
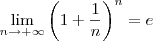
Genericamente:
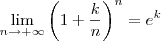
Podemos encarar isto como algo que sabemos de antemão que é verdadeiro, sem necessidade de provar.
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limites] como resolver utilizando L' Hôpital
por AboraBR » Qui Jul 12, 2012 15:33
- 2 Respostas
- 2036 Exibições
- Última mensagem por e8group

Qui Jul 12, 2012 17:16
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo: Limites, Derivadas e Integrais] Cálculo de limites
por jeferson lopes » Ter Mar 26, 2013 08:49
- 2 Respostas
- 5567 Exibições
- Última mensagem por jeferson lopes

Ter Mar 26, 2013 11:52
Cálculo: Limites, Derivadas e Integrais
-
- [limites] exercicio de calculo envolvendo limites
por lucasdemirand » Qua Jul 10, 2013 00:45
- 1 Respostas
- 4811 Exibições
- Última mensagem por e8group

Sáb Jul 20, 2013 13:08
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo 2 - Limites] Existência de Limites
por Piva » Seg Abr 16, 2012 11:29
- 0 Respostas
- 5448 Exibições
- Última mensagem por Piva

Seg Abr 16, 2012 11:29
Cálculo: Limites, Derivadas e Integrais
-
- L'Hôpital!
por talitaerika » Sex Mai 28, 2010 20:42
- 1 Respostas
- 1368 Exibições
- Última mensagem por Molina

Sex Mai 28, 2010 21:06
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
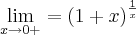

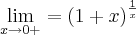

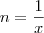 . Então
. Então 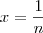
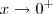 ,
,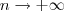 .
.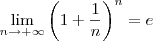
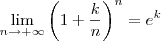

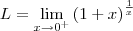
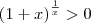 quando
quando 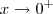 , podemos aplicar o logaritmo natural em ambos os membros dessa igualdade. Temos então que:
, podemos aplicar o logaritmo natural em ambos os membros dessa igualdade. Temos então que:![\ln L = \ln \left[\lim_{x\to 0^+} \left(1+x\right)^\frac{1}{x}\right] \ln L = \ln \left[\lim_{x\to 0^+} \left(1+x\right)^\frac{1}{x}\right]](/latexrender/pictures/8f625c93f12fd8933b542972a3a2dbe6.png)
![\ln L = \lim_{x\to 0^+} \ln \left[\left(1+x\right)^\frac{1}{x}\right] \ln L = \lim_{x\to 0^+} \ln \left[\left(1+x\right)^\frac{1}{x}\right]](/latexrender/pictures/20d56daceab41e8cb396217f33680a6c.png)
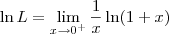
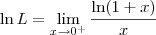
![\ln L = \lim_{x\to 0^+} \frac{[\ln (1+x)]^\prime}{(x)^\prime} \ln L = \lim_{x\to 0^+} \frac{[\ln (1+x)]^\prime}{(x)^\prime}](/latexrender/pictures/6c02e71751a4f00f9862360c75e4c7fd.png)
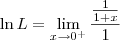
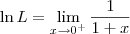
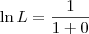



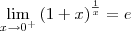


 .
.
 :
: