 por ant_dii » Qui Dez 01, 2011 03:10
por ant_dii » Qui Dez 01, 2011 03:10
Bom pessoal, este problema não é do ensino médio e nem é muito simples de resolver ( se o fosse eu já teria conseguido).
Terei que apresentá-lo resolvido semana que vem e já tem uns 5 dias que to quebrando a cabeça...
O problema é o seguinte:
Provar que se  e
e  são nulos, então
são nulos, então  é um campo de quadrado inverso.
é um campo de quadrado inverso.Eu acredito que há um erro no enunciado, que o que realmente vale é a recíproca, pois no caso do enunciado acima podemos ter

e

nulos, porém

um campo constante qualquer e não necessariamente (como indica) um campo de quadrado inverso :
Provar que se  é um campo de quadrado inverso, então
é um campo de quadrado inverso, então  e
e  são nulos.
são nulos.Já tentei de várias formas, até mesmo usando o Teorema de Gauss (Teorema da divergência) e o teorema de Stokes, mas não sei como proceder.
Se o enunciado estiver correto, eu acredito que o problema seja simples de resolver mas queria que me ajudassem a encontrar a melhor resposta...
Desde já agradece quem se disponibilizar.
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por LuizAquino » Sex Dez 02, 2011 16:37
por LuizAquino » Sex Dez 02, 2011 16:37
ant_dii escreveu:Provar que se

e

são nulos, então
F é um campo de quadrado inverso.
ant_dii escreveu:Eu acredito que há um erro no enunciado (...)
podemos ter

e

nulos, porém
F um campo constante qualquer e não necessariamente (como indica) um campo de quadrado inverso (...)
Ok.
ant_dii escreveu:(...) o que realmente vale é a recíproca:
Provar que se
F é um campo de quadrado inverso, então

e

são nulos.
ant_dii escreveu:Já tentei de várias formas, até mesmo usando o Teorema de Gauss (Teorema da divergência) e o teorema de Stokes, mas não sei como proceder.
Se
F é um campo de quadrado inverso (em três dimensões), então ele tem o formato:

,
com
c uma constante real.
Considerando que

, temos que:



Calculando o divergente, temos que:

Agora calcule as derivadas parciais e efetue a soma. Você irá obter que

.
Calculando o rotacional, temos que:

Agora calcule as derivadas parciais e efetue as subtrações. Você irá obter que

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por ant_dii » Sáb Dez 03, 2011 01:40
por ant_dii » Sáb Dez 03, 2011 01:40
Boa noite Luiz...
Obrigado pela disponibilidade...
Só incomodando um pouco novamente, quanto ao primeiro enunciado
Provar que se

e

são nulos, então F é um campo de quadrado inverso.
o que você me diz? Realmente esta errado ou esta simplesmente incompleto. Do meu ponto de vista esta incompleto sendo então necessário acrescentar que isso vale exceto quando F é constante ou nulo, mas não sei ainda se resolve pois ainda não consegui provar.
Conversei com um professor e ele me mostrou uma identidade interessante vinda do fato de que

e

são nulos. Vejamos, como você colocou acima:
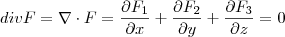
e

Fazendo

e

De onde,

que é a equação de Laplace em três dimensões, que esta estritamente ligada com o conceito de função potencial de campo de quadrado inverso, na verdade esta equação acima é satisfeita pelo campo de quadrado inverso

.
E agora o que você acha que devo fazer??
Obrigado desde já.
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por LuizAquino » Sáb Dez 03, 2011 11:16
por LuizAquino » Sáb Dez 03, 2011 11:16
ant_dii escreveu:Provar que se

e

são nulos, então
F é um campo de quadrado inverso.
o que você me diz? Realmente esta errado ou esta simplesmente incompleto.
Do meu ponto de vista esta incompleto sendo então necessário acrescentar que isso vale exceto quando F é constante ou nulo, mas não sei ainda se resolve pois ainda não consegui provar.
Mesmo que
F não seja constante, ainda podemos ter o divergente e o rotacional de
F nulos, mas de modo que
F não seja um campo de quadrado inverso.
Por exemplo, considere

. Note que

e

, mas
F não é constante e não é um campo de quadrado inverso.
ant_dii escreveu:De onde,

que é a equação de Laplace em três dimensões, que esta estritamente ligada com o conceito de função potencial de campo de quadrado inverso, na verdade esta equação acima é satisfeita pelo campo de quadrado inverso

.
Note que essa equação também é satisfeita para outros campos
F que não são de quadrado inverso. Por exemplo, ela é satisfeita para o mesmo
F dado acima:

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por ant_dii » Sáb Dez 03, 2011 11:39
por ant_dii » Sáb Dez 03, 2011 11:39
Luiz,
Obrigado novamente.
A questão é que de fato a função potencial do campo de quadrado inverso satisfaz a equação acima (equação de Laplace).
Ela tem uma condição sobre sua formulação, a de que a função tem que ser duplamente diferenciável e contínua, ou seja, tem que pertencer ao conjunto das funções de classe
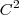
.
Mas já entendi e encontrei um caminho para apresentar a resolução do problema.
Muito obrigado mesmo por disponibilizar seu tempo.
Até mais.
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Análise Combinatória] Quadrado 4x4
 por Gustavo Gomes » Qua Mai 07, 2014 23:28
por Gustavo Gomes » Qua Mai 07, 2014 23:28
- 0 Respostas
- 1646 Exibições
- Última mensagem por Gustavo Gomes

Qua Mai 07, 2014 23:28
Análise Combinatória
-
- Trinomio Quadrado Perfeito (Complemento de quadrado)
por IgorFilipe » Qua Ago 17, 2011 23:01
- 2 Respostas
- 3753 Exibições
- Última mensagem por IgorFilipe

Qui Ago 18, 2011 15:52
Funções
-
- inverso da potência
por aynee » Sex Jul 18, 2014 12:37
- 2 Respostas
- 2090 Exibições
- Última mensagem por aynee

Sex Jul 18, 2014 18:35
Álgebra Elementar
-
- TÓPICO DE DÚVIDAS DO CHAT
por Molina » Ter Fev 17, 2009 23:11
- 4 Respostas
- 5122 Exibições
- Última mensagem por Molina

Qui Abr 16, 2009 21:27
Tópicos sem Interação (leia as regras)
-
- eliminar este tópico
por anaqs » Qui Jun 25, 2015 14:12
- 0 Respostas
- 2933 Exibições
- Última mensagem por anaqs

Sáb Jul 25, 2015 19:23
Desafios Difíceis
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e
e  são nulos, então
são nulos, então  é um campo de quadrado inverso.
é um campo de quadrado inverso. e
e  nulos, porém
nulos, porém  um campo constante qualquer e não necessariamente (como indica) um campo de quadrado inverso :
um campo constante qualquer e não necessariamente (como indica) um campo de quadrado inverso : é um campo de quadrado inverso, então
é um campo de quadrado inverso, então  e
e  são nulos.
são nulos.

 e
e  ,
, , temos que:
, temos que:



 .
.
 .
.
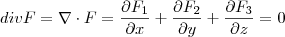




 .
. . Note que
. Note que 
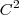 .
.

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.