odra1974 escreveu:Estou tentando faz um dia e não consigo resolver a integral
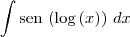
(...)
Cheguei até aqui e acho que não dá saida para eliminar a integral, pois parece que entra num ciclo vicioso
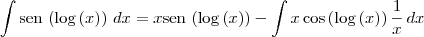
Você está usando a convenção de que

representa o logaritmo natural? Isto é, o logaritmo na base
e?
Se for isso, então de fato você pode usar que
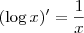
quando aplicar a integração por partes.
Mas se por outro lado você está usando a convenção de que

representa o logaritmo na base 10, então lembre-se que
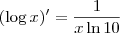
(onde aqui "ln" representa o logaritmo natural -- ou seja, na base
e).
Vou considerar que você está usando a convenção de que

representa
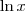
.
Para continuar a resolução, faça
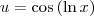
e

. Dessa forma, note que:
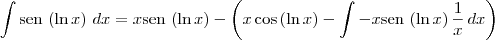
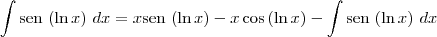
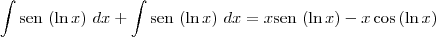
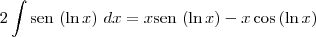
![\int \textrm{sen}\,\left(\ln x \right)\,dx = \frac{1}{2}\left[x \textrm{sen}\,\left(\ln x \right) - x\cos \left( \ln x \right)\right] + c \int \textrm{sen}\,\left(\ln x \right)\,dx = \frac{1}{2}\left[x \textrm{sen}\,\left(\ln x \right) - x\cos \left( \ln x \right)\right] + c](/latexrender/pictures/967e4650bdf1f6849f36a5758483c6d4.png)
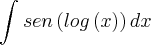
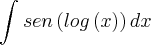 =
=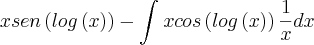


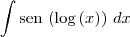
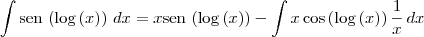
 representa o logaritmo natural? Isto é, o logaritmo na base
representa o logaritmo natural? Isto é, o logaritmo na base 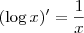 quando aplicar a integração por partes.
quando aplicar a integração por partes.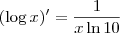 (onde aqui "ln" representa o logaritmo natural -- ou seja, na base
(onde aqui "ln" representa o logaritmo natural -- ou seja, na base 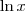 .
.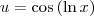 e
e  . Dessa forma, note que:
. Dessa forma, note que: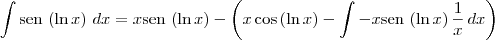
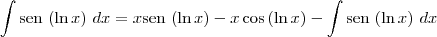
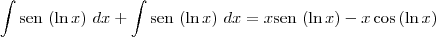
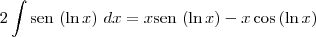
![\int \textrm{sen}\,\left(\ln x \right)\,dx = \frac{1}{2}\left[x \textrm{sen}\,\left(\ln x \right) - x\cos \left( \ln x \right)\right] + c \int \textrm{sen}\,\left(\ln x \right)\,dx = \frac{1}{2}\left[x \textrm{sen}\,\left(\ln x \right) - x\cos \left( \ln x \right)\right] + c](/latexrender/pictures/967e4650bdf1f6849f36a5758483c6d4.png)

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)