Antes de mais, peço desculpa se o exercício não foi colocado no local correto, mas estou com algumas dificuldades em resolvê-lo.
O exercício é o seguinte:
8.) O modelo matemático encontrado para descrever o arco de entrada num túnel, representado no referencial o.n xOy , é dado pela função:
f(x) =ln (16-x^2)(x elevado a 2)
8.1) Recorra à calculadora gráfica para determinar o ponto onde a taxa de variação de f é nula e interprete o valor encontrado no contexto do problema.
8.2) Determine a distância ___ (a largura da entrada do túnel).
-------------------------------- AB
A imagem referente ao exercício é esta:
Tenho imensas dúvidas do que fazer neste exercício, daí não ter colocado nenhuma explicação no contexto em si.
Agradeço a quem me ajudar a resolvê-lo, pois terei que o apresentar amanhã, muito obrigado!
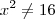e 
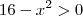. Dessas duas, podemos obter que 
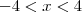(explicação detalhada: 
).
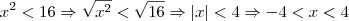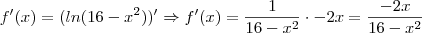
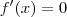, ou seja, 
.
.
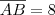por