 por adauto martins » Sáb Out 26, 2019 19:46
por adauto martins » Sáb Out 26, 2019 19:46
(ENE-escola nacional de engenharia da universidade do brasil,rj-exame de ad.1958)
calcule a area compreendida entre as curvas

e
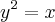
.
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Sáb Out 26, 2019 20:09
por adauto martins » Sáb Out 26, 2019 20:09
soluçao:
primeiramente temos que ter

,pois

.
vamos achar os pontos onde essas curvas se interceptam...temos:
![y=\sqrt[]{x}...y={x}^{2}
\sqrt[]{x}={x}^{2} y=\sqrt[]{x}...y={x}^{2}
\sqrt[]{x}={x}^{2}](/latexrender/pictures/d161882409fd4925b3674ca336690339.png)
![{x}^{4}-x=0\Rightarrow x({x}^{3}-1)=0
x=0...x=\sqrt[]{1}=1...x,y\in \Re {x}^{4}-x=0\Rightarrow x({x}^{3}-1)=0
x=0...x=\sqrt[]{1}=1...x,y\in \Re](/latexrender/pictures/a09f3c5c92301949adf52f316da71147.png)
para calcular a area pedida,que é dada por:
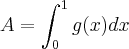
onde
![g(x)=\sqrt[]{x}-{x}^{2} g(x)=\sqrt[]{x}-{x}^{2}](/latexrender/pictures/046c6983fa3c90d96f9642e5b7008483.png)
, pois
![\sqrt[]{x}\geq {x}^{2} \sqrt[]{x}\geq {x}^{2}](/latexrender/pictures/f9146ddfddad8f5e265edeb9838fe6e6.png)
...(pq?)
logo:
![A=\int_{0}^{1}(\sqrt[]{x}-{x}^{2})dx=\int_{0}^{1}(\sqrt[]{x})dx-\int_{0}^{1}{x}^{2}dx=
A=(1/(1/2)+1){x}^{(1/2+1)}[0,1]-(1/(2+1)){x}^{1+2}[0,1]=
=(2/3){x}^{3/2}[0,1]-(1/3){x}^{3}[0,1]=...=(2/3)-(1/3)=1/3 A=\int_{0}^{1}(\sqrt[]{x}-{x}^{2})dx=\int_{0}^{1}(\sqrt[]{x})dx-\int_{0}^{1}{x}^{2}dx=
A=(1/(1/2)+1){x}^{(1/2+1)}[0,1]-(1/(2+1)){x}^{1+2}[0,1]=
=(2/3){x}^{3/2}[0,1]-(1/3){x}^{3}[0,1]=...=(2/3)-(1/3)=1/3](/latexrender/pictures/03f7353edea5c10f8d145d4c2792572f.png)
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e
e 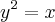 .
.
 e
e 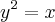 .
.
 ,pois
,pois  .
.![y=\sqrt[]{x}...y={x}^{2}
\sqrt[]{x}={x}^{2} y=\sqrt[]{x}...y={x}^{2}
\sqrt[]{x}={x}^{2}](/latexrender/pictures/d161882409fd4925b3674ca336690339.png)
![{x}^{4}-x=0\Rightarrow x({x}^{3}-1)=0
x=0...x=\sqrt[]{1}=1...x,y\in \Re {x}^{4}-x=0\Rightarrow x({x}^{3}-1)=0
x=0...x=\sqrt[]{1}=1...x,y\in \Re](/latexrender/pictures/a09f3c5c92301949adf52f316da71147.png)
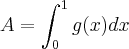
![g(x)=\sqrt[]{x}-{x}^{2} g(x)=\sqrt[]{x}-{x}^{2}](/latexrender/pictures/046c6983fa3c90d96f9642e5b7008483.png) , pois
, pois ![\sqrt[]{x}\geq {x}^{2} \sqrt[]{x}\geq {x}^{2}](/latexrender/pictures/f9146ddfddad8f5e265edeb9838fe6e6.png) ...(pq?)
...(pq?)![A=\int_{0}^{1}(\sqrt[]{x}-{x}^{2})dx=\int_{0}^{1}(\sqrt[]{x})dx-\int_{0}^{1}{x}^{2}dx=
A=(1/(1/2)+1){x}^{(1/2+1)}[0,1]-(1/(2+1)){x}^{1+2}[0,1]=
=(2/3){x}^{3/2}[0,1]-(1/3){x}^{3}[0,1]=...=(2/3)-(1/3)=1/3 A=\int_{0}^{1}(\sqrt[]{x}-{x}^{2})dx=\int_{0}^{1}(\sqrt[]{x})dx-\int_{0}^{1}{x}^{2}dx=
A=(1/(1/2)+1){x}^{(1/2+1)}[0,1]-(1/(2+1)){x}^{1+2}[0,1]=
=(2/3){x}^{3/2}[0,1]-(1/3){x}^{3}[0,1]=...=(2/3)-(1/3)=1/3](/latexrender/pictures/03f7353edea5c10f8d145d4c2792572f.png)
