 por andersonsg » Seg Jun 15, 2015 15:17
por andersonsg » Seg Jun 15, 2015 15:17
Bom dia.
Estou levando uma surra deste exercício, se alguém puder me ajudar eu agradeço.
Calcular a derivada parcial em relação a y da f(x,y) = \frac{1}{r}(\frac{-y}{2} + \frac{x}{2} \sqrt[2]{\frac{4{r}^{2}}{{x}^{2}+{y}^{2}}-1}).
Obrigado.
-
andersonsg
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Jun 15, 2015 13:03
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Eletrica
- Andamento: cursando
 por nakagumahissao » Sáb Jul 18, 2015 11:33
por nakagumahissao » Sáb Jul 18, 2015 11:33
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12556 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [derivada] derivada pela definição da secante
por TheKyabu » Sáb Out 27, 2012 23:24
- 2 Respostas
- 10896 Exibições
- Última mensagem por TheKyabu

Dom Out 28, 2012 11:44
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Com duas variáveis e derivada mista
por leticiaeverson » Dom Abr 22, 2018 00:39
- 3 Respostas
- 13201 Exibições
- Última mensagem por Gebe

Dom Abr 22, 2018 17:11
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada]derivada de função de raiz cúbica
por armando » Sáb Jul 20, 2013 15:22
- 4 Respostas
- 14807 Exibições
- Última mensagem por armando

Dom Jul 21, 2013 22:17
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] DERIVADA POR DEFINIÇÃO DA RAIZ DO MÓDULO DE X
por Matheusgdp » Qua Set 16, 2015 04:07
- 2 Respostas
- 5117 Exibições
- Última mensagem por Matheusgdp

Qui Set 17, 2015 18:31
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



![f(x,y) = \frac{1}{r}(\frac{-y}{2} + \frac{x}{2} \sqrt[2]{\frac{4{r}^{2}}{{x}^{2}+{y}^{2}}-1}) f(x,y) = \frac{1}{r}(\frac{-y}{2} + \frac{x}{2} \sqrt[2]{\frac{4{r}^{2}}{{x}^{2}+{y}^{2}}-1})](/latexrender/pictures/9a430824244782704ef4982304ae823c.png)
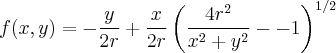
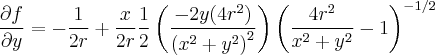
![\frac{\partial f}{\partial y} = -\frac{1}{2r} + \frac{x}{4r}\left[\frac{-8r^2 y}{{(x^2 + y^2)}^{2}} \right]\frac{1}{\left(\frac{4r^2}{x^2 + y^2} - 1 \right) ^{1/2}} \frac{\partial f}{\partial y} = -\frac{1}{2r} + \frac{x}{4r}\left[\frac{-8r^2 y}{{(x^2 + y^2)}^{2}} \right]\frac{1}{\left(\frac{4r^2}{x^2 + y^2} - 1 \right) ^{1/2}}](/latexrender/pictures/cca05ccd5ec6929021f7f816f47e45ae.png)
![\frac{\partial f}{\partial y} = -\frac{1}{2r} - x\left[\frac{2r y}{{(x^2 + y^2)}^{2}} \right]\frac{1}{\sqrt[]{\frac{4r^2}{x^2 + y^2} - 1}} \frac{\partial f}{\partial y} = -\frac{1}{2r} - x\left[\frac{2r y}{{(x^2 + y^2)}^{2}} \right]\frac{1}{\sqrt[]{\frac{4r^2}{x^2 + y^2} - 1}}](/latexrender/pictures/5c34f7f3198089cb3faeaecf6ec486d6.png)


 .
.
 :
: