 por ViniciusAlmeida » Seg Mai 04, 2015 09:24
por ViniciusAlmeida » Seg Mai 04, 2015 09:24
Calcular o limite:

Eu tentei dividir o numerador e o denominador por x:

Mas aplicando a propriedade tanto numerador quanto denominador vão zerar e o gabarito é +infinito
Qual meu erro?
-
ViniciusAlmeida
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Seg Fev 09, 2015 12:13
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por adauto martins » Ter Mai 05, 2015 19:13
por adauto martins » Ter Mai 05, 2015 19:13
![L=\lim_{x\rightarrow -\infty}x.(\sqrt[]{1+2/{x}^{2}}-1)=-\infty.0 L=\lim_{x\rightarrow -\infty}x.(\sqrt[]{1+2/{x}^{2}}-1)=-\infty.0](/latexrender/pictures/5f57575aa77c05a03b3b4069c0c76f5d.png)
,q. eh uma indeterminaçao...logo vamos usar a regra de l'hospital...podemoas fazer assim...
![L=\lim_{x\rightarrow -\infty}(\sqrt[]{1+2/{x}^{2}}-1)/(1/x) L=\lim_{x\rightarrow -\infty}(\sqrt[]{1+2/{x}^{2}}-1)/(1/x)](/latexrender/pictures/73e5c06ebccb0510dad58420f9f7d0f5.png)
q. ficaria...
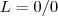
,apartir dai e fazer...
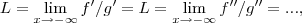
,onde,
![f(x)=\sqrt[]{1+2/{x}^{2}}-1,g(x)=1/x f(x)=\sqrt[]{1+2/{x}^{2}}-1,g(x)=1/x](/latexrender/pictures/c909b264f9cb8796b49753672040436d.png)
ir derivando ate achar um valor fixo...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6650 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4793 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5126 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7267 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4445 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






![L=\lim_{x\rightarrow -\infty}x.(\sqrt[]{1+2/{x}^{2}}-1)=-\infty.0 L=\lim_{x\rightarrow -\infty}x.(\sqrt[]{1+2/{x}^{2}}-1)=-\infty.0](/latexrender/pictures/5f57575aa77c05a03b3b4069c0c76f5d.png) ,q. eh uma indeterminaçao...logo vamos usar a regra de l'hospital...podemoas fazer assim...
,q. eh uma indeterminaçao...logo vamos usar a regra de l'hospital...podemoas fazer assim...![L=\lim_{x\rightarrow -\infty}(\sqrt[]{1+2/{x}^{2}}-1)/(1/x) L=\lim_{x\rightarrow -\infty}(\sqrt[]{1+2/{x}^{2}}-1)/(1/x)](/latexrender/pictures/73e5c06ebccb0510dad58420f9f7d0f5.png) q. ficaria...
q. ficaria...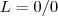 ,apartir dai e fazer...
,apartir dai e fazer...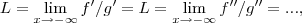 ,onde,
,onde,![f(x)=\sqrt[]{1+2/{x}^{2}}-1,g(x)=1/x f(x)=\sqrt[]{1+2/{x}^{2}}-1,g(x)=1/x](/latexrender/pictures/c909b264f9cb8796b49753672040436d.png) ir derivando ate achar um valor fixo...
ir derivando ate achar um valor fixo...

 .
.



