O problema é o seguinte. Limite
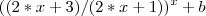quando x->infinito. sendo x pertencente aos reais.A resposta é E, ou seja numero de Euler.
Pelo que sei, se deve "transforma" a equação acima em uma lim X-> +infinito (1+1/x)^x para que se tenha o "E" como resultado.
eu tentei varias formas, mas todas terminaram em indeterminações e nem perto de E.
Se possível, gostaria de uma ajuda.
Obs: a equação toda é elevada a X+B, não sei usa muito bem a linguagem LaTeX.
por 
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será 
, então 
. Como módulo é um: 
.
.