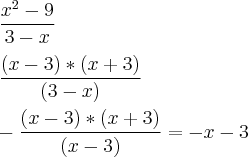Para cada função f a seguir, determine D(f) e, se possível, a função g: R->R, tal que g é contínua e g(x) = f(x), para todo x pertencente D(x):
a)
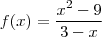
eu fiz da seguinte forma: como ele fala que g(x)=f(x) eu fui usando o f(x), e acho que estou errado nessa parte. Logo eu fiz o seguinte.
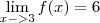
porém o f(3) não está definido..quando eu faço dá uma indeterminação (não sei se para este caso tem que tirar a indeterminação) porém, sou leigo em calculo, comecei agora. Eu queria entender essa questão, desde já agradeço..preciso muito dessa questão até amanhã..se alguem puder muito me ajudar..obrigado



 :
: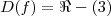 que é o conjunto dos números reais exceto 3 que zeraria o denominador,já para obter uma função g(x) contínua e g(x) = f(x), para todo x pertencente ao dominio de f(x) :
que é o conjunto dos números reais exceto 3 que zeraria o denominador,já para obter uma função g(x) contínua e g(x) = f(x), para todo x pertencente ao dominio de f(x) :