 por Jhenrique » Sex Mai 24, 2013 18:19
por Jhenrique » Sex Mai 24, 2013 18:19
Eae gente, blz!?
Vendo este vídeo (no exato instante do link (
http://www.youtube.com/watch?v=kQb6T5MiRLM?t=9m30s)), tem-se a seguinte igualdade:

Essa igualdade é uma convenção física quantitativa, quero dizer, uma simples equação, como:
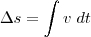
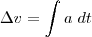
Ou é uma regra matemática? Quero dizer... a integral sempre resulta num delta não-infinitesimal? Seria este delta um subterfúgio para omitir a adição da constante de integração?
Obg!
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por Russman » Sex Mai 24, 2013 20:10
por Russman » Sex Mai 24, 2013 20:10
A constante de integração voce adiciona na integral indefinida. As sua integrais estão indefinidas e a variação que voce esta escrevendo não faz sentido.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Jhenrique » Sáb Mai 25, 2013 17:13
por Jhenrique » Sáb Mai 25, 2013 17:13
A variações deltas eu tirei do vídeo que eu postei e do dicionário de Física Houaiss:

Está bem miudinho mas dá para ler, acho...
Sempre fico confuso quando tento fazer "análise sintática" em integrais...
Certos problemas também já me levaram a pensar se
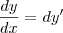
em vez de
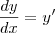
...
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Achar o [tex]\delta[/tex].
por filipeferminiano » Qui Ago 26, 2010 16:42
- 2 Respostas
- 2083 Exibições
- Última mensagem por filipeferminiano

Sex Ago 27, 2010 00:30
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Determinar um delta
por caiofisico » Sáb Ago 20, 2011 22:38
- 4 Respostas
- 4539 Exibições
- Última mensagem por caiofisico

Seg Ago 22, 2011 19:00
Cálculo: Limites, Derivadas e Integrais
-
- Inequação - 2º grau com delta menor que zero
por renanrdaros » Sex Mar 25, 2011 18:27
- 8 Respostas
- 7446 Exibições
- Última mensagem por johnlaw

Dom Mar 27, 2011 16:33
Álgebra Elementar
-
- Raiz quadrada do discriminante ?Delta
por IgorFilipe » Ter Ago 23, 2011 17:13
- 7 Respostas
- 5477 Exibições
- Última mensagem por LuizAquino

Sáb Ago 27, 2011 13:07
Funções
-
- (Equação de 2° grau) com o Delta sem valor exato
por morcego265 » Sáb Jul 27, 2013 13:48
- 1 Respostas
- 1521 Exibições
- Última mensagem por DanielFerreira

Sáb Ago 03, 2013 08:48
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

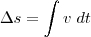
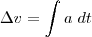



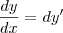 em vez de
em vez de 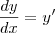 ...
... .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
