 por ARCS » Qui Out 28, 2010 19:27
por ARCS » Qui Out 28, 2010 19:27
Boa Noite,
Gostaria que alguem explica-se como resolver essa questão de limite
SEM USAR o artifício de substituição de variáveis.
PS: Sei resolver usando o artíficio de substituição, meu professor resolveu na aula sem usa-lo, porém não entendi.
Expliquem detalhadamente para que eu possa entender!
Grato.
![\lim_{x\rightarrow0}\frac{\sqrt[3]{x+1}-1}{x} \lim_{x\rightarrow0}\frac{\sqrt[3]{x+1}-1}{x}](/latexrender/pictures/f27032f84d4e9b30903669cf6318c076.png)
-
ARCS
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Qui Out 28, 2010 18:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por victoreis1 » Qui Out 28, 2010 20:02
por victoreis1 » Qui Out 28, 2010 20:02
Boa noite.. se vc já aprendeu derivadas, use a regra de L'Hôpital, transformando o limite em
![\lim_{x\to0} \frac{\frac{d}{dx}(\sqrt[3]{x+1} -1)}{\frac{dx}{dx}} \lim_{x\to0} \frac{\frac{d}{dx}(\sqrt[3]{x+1} -1)}{\frac{dx}{dx}}](/latexrender/pictures/e29527a1f686e5e7c56b329526d9978c.png)
sabe-se que a derivada de x é 1 e a de (-1) é zero.. logo o limite é igual a
![\lim_{x\to0} {\frac{d}{dx}(\sqrt[3]{x+1})} \lim_{x\to0} {\frac{d}{dx}(\sqrt[3]{x+1})}](/latexrender/pictures/2aa2835b554a3a120ca6c9303c8d9b26.png)
Não sei muito de derivadas.. se souber calcular, vê aí se dá certo (:
-
victoreis1
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qua Out 20, 2010 14:49
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Qui Out 28, 2010 22:30
por MarceloFantini » Qui Out 28, 2010 22:30
Use fatoração de cubos:
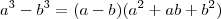
. Você já tem um termo, agora multiplique numerador e denominador pelo outro.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6650 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4795 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5126 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7268 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4446 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow0}\frac{\sqrt[3]{x+1}-1}{x} \lim_{x\rightarrow0}\frac{\sqrt[3]{x+1}-1}{x}](/latexrender/pictures/f27032f84d4e9b30903669cf6318c076.png)


![\lim_{x\to0} \frac{\frac{d}{dx}(\sqrt[3]{x+1} -1)}{\frac{dx}{dx}} \lim_{x\to0} \frac{\frac{d}{dx}(\sqrt[3]{x+1} -1)}{\frac{dx}{dx}}](/latexrender/pictures/e29527a1f686e5e7c56b329526d9978c.png)
![\lim_{x\to0} {\frac{d}{dx}(\sqrt[3]{x+1})} \lim_{x\to0} {\frac{d}{dx}(\sqrt[3]{x+1})}](/latexrender/pictures/2aa2835b554a3a120ca6c9303c8d9b26.png)
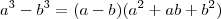 . Você já tem um termo, agora multiplique numerador e denominador pelo outro.
. Você já tem um termo, agora multiplique numerador e denominador pelo outro.


 .
.
 :
: