![\lim_{x\rightarrow0} \frac{3{x}^{2}-8}{x-2}
\lim_{x\rightarrow2} \left( 3{x}^{2}-5x+2\right)
\lim_{x\rightarrow0} \left({x}^{5}-6{x}^{4}+7 \right)
\lim_{x\rightarrow3} \left({x-1}^{2} \right)\left(x+1 \right)
\lim_{x\rightarrow5} \frac{x+3}{5-x}
\lim_{x\rightarrow2} \frac{x+1}{x+2}
\lim_{x\rightarrow1} \frac{{x}^{2}-1}{x-1}
\lim_{x\rightarrow5} \frac{x+3}{5-x}
\lim_{x\rightarrow2} \frac{x+1}{x+2}
\lim_{x\rightarrow1} \frac{{x}^{2}-1}{x-1}
\lim_{x\rightarrow2} \frac{{x}^{2}-x-6}{{x}^{2}+3x+2}
\lim_{x\rightarrow4} \frac{\sqrt[]{x}-2}{x-4}
\lim_{x\rightarrow3} \frac{{x}^{2}-9}{x-3}
\lim_{x\rightarrow1} \frac{{x}^{2} +4x-5}{{x}^{2}-1}
\lim_{x\rightarrow1} \frac{\sqrt[]{x}-1}{x-1}
\lim_{x\rightarrow4} \frac{\sqrt[]{x}-2}{x-4}
\lim_{x\rightarrow9} \frac{\sqrt[]{x}-3}{x-9}
\lim_{x\rightarrow2} \frac{{x}^{3}-8}{{x}^{2}-4}
\lim_{x\rightarrow2} \frac{{x}^{3}-8x+8}{{3x}^{3}-{15x}^{2}+16x+4} \lim_{x\rightarrow0} \frac{3{x}^{2}-8}{x-2}
\lim_{x\rightarrow2} \left( 3{x}^{2}-5x+2\right)
\lim_{x\rightarrow0} \left({x}^{5}-6{x}^{4}+7 \right)
\lim_{x\rightarrow3} \left({x-1}^{2} \right)\left(x+1 \right)
\lim_{x\rightarrow5} \frac{x+3}{5-x}
\lim_{x\rightarrow2} \frac{x+1}{x+2}
\lim_{x\rightarrow1} \frac{{x}^{2}-1}{x-1}
\lim_{x\rightarrow5} \frac{x+3}{5-x}
\lim_{x\rightarrow2} \frac{x+1}{x+2}
\lim_{x\rightarrow1} \frac{{x}^{2}-1}{x-1}
\lim_{x\rightarrow2} \frac{{x}^{2}-x-6}{{x}^{2}+3x+2}
\lim_{x\rightarrow4} \frac{\sqrt[]{x}-2}{x-4}
\lim_{x\rightarrow3} \frac{{x}^{2}-9}{x-3}
\lim_{x\rightarrow1} \frac{{x}^{2} +4x-5}{{x}^{2}-1}
\lim_{x\rightarrow1} \frac{\sqrt[]{x}-1}{x-1}
\lim_{x\rightarrow4} \frac{\sqrt[]{x}-2}{x-4}
\lim_{x\rightarrow9} \frac{\sqrt[]{x}-3}{x-9}
\lim_{x\rightarrow2} \frac{{x}^{3}-8}{{x}^{2}-4}
\lim_{x\rightarrow2} \frac{{x}^{3}-8x+8}{{3x}^{3}-{15x}^{2}+16x+4}](/latexrender/pictures/11aca0072a8cf2a1efa5de04de8cb065.png)
Pessoal, por favor, me ajudem a resolver estas questões de limite, estou precisando muito.

![\lim_{x\rightarrow0} \frac{3{x}^{2}-8}{x-2}
\lim_{x\rightarrow2} \left( 3{x}^{2}-5x+2\right)
\lim_{x\rightarrow0} \left({x}^{5}-6{x}^{4}+7 \right)
\lim_{x\rightarrow3} \left({x-1}^{2} \right)\left(x+1 \right)
\lim_{x\rightarrow5} \frac{x+3}{5-x}
\lim_{x\rightarrow2} \frac{x+1}{x+2}
\lim_{x\rightarrow1} \frac{{x}^{2}-1}{x-1}
\lim_{x\rightarrow5} \frac{x+3}{5-x}
\lim_{x\rightarrow2} \frac{x+1}{x+2}
\lim_{x\rightarrow1} \frac{{x}^{2}-1}{x-1}
\lim_{x\rightarrow2} \frac{{x}^{2}-x-6}{{x}^{2}+3x+2}
\lim_{x\rightarrow4} \frac{\sqrt[]{x}-2}{x-4}
\lim_{x\rightarrow3} \frac{{x}^{2}-9}{x-3}
\lim_{x\rightarrow1} \frac{{x}^{2} +4x-5}{{x}^{2}-1}
\lim_{x\rightarrow1} \frac{\sqrt[]{x}-1}{x-1}
\lim_{x\rightarrow4} \frac{\sqrt[]{x}-2}{x-4}
\lim_{x\rightarrow9} \frac{\sqrt[]{x}-3}{x-9}
\lim_{x\rightarrow2} \frac{{x}^{3}-8}{{x}^{2}-4}
\lim_{x\rightarrow2} \frac{{x}^{3}-8x+8}{{3x}^{3}-{15x}^{2}+16x+4} \lim_{x\rightarrow0} \frac{3{x}^{2}-8}{x-2}
\lim_{x\rightarrow2} \left( 3{x}^{2}-5x+2\right)
\lim_{x\rightarrow0} \left({x}^{5}-6{x}^{4}+7 \right)
\lim_{x\rightarrow3} \left({x-1}^{2} \right)\left(x+1 \right)
\lim_{x\rightarrow5} \frac{x+3}{5-x}
\lim_{x\rightarrow2} \frac{x+1}{x+2}
\lim_{x\rightarrow1} \frac{{x}^{2}-1}{x-1}
\lim_{x\rightarrow5} \frac{x+3}{5-x}
\lim_{x\rightarrow2} \frac{x+1}{x+2}
\lim_{x\rightarrow1} \frac{{x}^{2}-1}{x-1}
\lim_{x\rightarrow2} \frac{{x}^{2}-x-6}{{x}^{2}+3x+2}
\lim_{x\rightarrow4} \frac{\sqrt[]{x}-2}{x-4}
\lim_{x\rightarrow3} \frac{{x}^{2}-9}{x-3}
\lim_{x\rightarrow1} \frac{{x}^{2} +4x-5}{{x}^{2}-1}
\lim_{x\rightarrow1} \frac{\sqrt[]{x}-1}{x-1}
\lim_{x\rightarrow4} \frac{\sqrt[]{x}-2}{x-4}
\lim_{x\rightarrow9} \frac{\sqrt[]{x}-3}{x-9}
\lim_{x\rightarrow2} \frac{{x}^{3}-8}{{x}^{2}-4}
\lim_{x\rightarrow2} \frac{{x}^{3}-8x+8}{{3x}^{3}-{15x}^{2}+16x+4}](/latexrender/pictures/11aca0072a8cf2a1efa5de04de8cb065.png)
[O anexo não pode ser exibido, pois a extensão pdf foi desativada pelo administrador.]

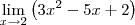
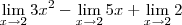



Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.



