U
![(x1,x2)= \left[\alpha1{x1}^{\rho}.a2{x2}^{\rho} \right]^{\frac{1}{p}} (x1,x2)= \left[\alpha1{x1}^{\rho}.a2{x2}^{\rho} \right]^{\frac{1}{p}}](/latexrender/pictures/b9ea18b2fad16d6b636d6f2e341139aa.png)
Deriavada - Taxa marginal de substituição (x,y) =
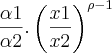
Fica na seguinte equação - d=derivada
![\frac{d \frac{x2}{x1}}{d \left[\frac{\alpha1}{\alpha2}\left(\frac{x1}{x2}\right)^{\rho-1} \right]}. \frac{\frac{\alpha1}{\alpha2}\left(\frac{x1}{x2}\right)^{\rho-1} }{\frac{x2}{x1}} \frac{d \frac{x2}{x1}}{d \left[\frac{\alpha1}{\alpha2}\left(\frac{x1}{x2}\right)^{\rho-1} \right]}. \frac{\frac{\alpha1}{\alpha2}\left(\frac{x1}{x2}\right)^{\rho-1} }{\frac{x2}{x1}}](/latexrender/pictures/71b00d17f8a412c9e01fb76dc6d70f75.png)
Eu quero saber porque se chega nessa equação
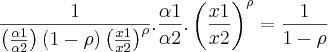
Eu queria saber porque apareceu o
 e o
e o 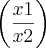 fica só elevado a
fica só elevado a 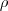 eo
eo  porque some.
porque some. Tem o
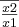 que some também não sei porque?
que some também não sei porque?Alguém pode resolver essa equação? Eu não consigo




 .
.
 :
: