 por adauto martins » Qua Out 23, 2019 20:56
por adauto martins » Qua Out 23, 2019 20:56
(EN-escola naval-exame?)
sejam f e g duas funçoes reais e derivaveis tais que
![f'(x)=sen(cos\sqrt[]{x}) f'(x)=sen(cos\sqrt[]{x})](/latexrender/pictures/c68c7e3e709155d641110f4a8caff361.png)
e
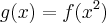
,
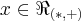
.pode-se afirmar
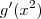
é igual a:
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Qua Out 23, 2019 21:12
por adauto martins » Qua Out 23, 2019 21:12
soluçao:
pelos dados do problema,temos que:
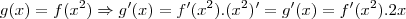
,
aqui usando a "regra da cadeia das funçoes compostas"...logo:
![g'(x)=f'({x}^{2}).2x=f'(sen(cos\sqrt[]{({x}^{2})}).2x
g'(x)=f'(sen(cosx)).2x g'(x)=f'({x}^{2}).2x=f'(sen(cos\sqrt[]{({x}^{2})}).2x
g'(x)=f'(sen(cosx)).2x](/latexrender/pictures/a30d15e98866d3e7f98d79a8aa917fab.png)
...
portanto:
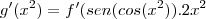
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![f'(x)=sen(cos\sqrt[]{x}) f'(x)=sen(cos\sqrt[]{x})](/latexrender/pictures/c68c7e3e709155d641110f4a8caff361.png) e
e 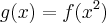 ,
,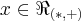 .pode-se afirmar
.pode-se afirmar 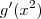 é igual a:
é igual a:
![f'(x)=sen(cos\sqrt[]{x}) f'(x)=sen(cos\sqrt[]{x})](/latexrender/pictures/c68c7e3e709155d641110f4a8caff361.png) e
e 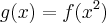 ,
,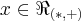 .pode-se afirmar
.pode-se afirmar 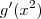 é igual a:
é igual a:
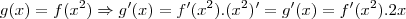 ,
,![g'(x)=f'({x}^{2}).2x=f'(sen(cos\sqrt[]{({x}^{2})}).2x
g'(x)=f'(sen(cosx)).2x g'(x)=f'({x}^{2}).2x=f'(sen(cos\sqrt[]{({x}^{2})}).2x
g'(x)=f'(sen(cosx)).2x](/latexrender/pictures/a30d15e98866d3e7f98d79a8aa917fab.png) ...
...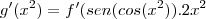

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)