 por jurexjurex » Seg Mar 07, 2016 07:16
por jurexjurex » Seg Mar 07, 2016 07:16
Um muro tem 3 m de altura, é paralelo à parede de um edifício e está a 0,30 m desta. Determine o comprimento da menor escada que vá do chão à parede do edifício, tocando o muro.
-
jurexjurex
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Mar 07, 2016 07:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por adauto martins » Dom Mar 13, 2016 12:48
por adauto martins » Dom Mar 13, 2016 12:48
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Dom Mar 13, 2016 13:36
por adauto martins » Dom Mar 13, 2016 13:36
caro colegas,aqui fiço o calculo da escada esta entre o muro e a parede...o problema nao especificou bem onde a escada estava...farei o calculo da escada por fora do muro...
vou postar depois,tdbem...obrigado
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Seg Mar 14, 2016 10:40
por adauto martins » Seg Mar 14, 2016 10:40
vamos usar semelhança de triangulos para obter medidas em funçao de medidas...
chamaremos y=altura ,x=distancia maior do triangulo maior...logo...
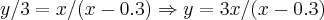
,entao obtivemos y=f(x)...
o comprim. da escada sera dado pela hipotenusa do triangulo maior...
![c(x,y)=\sqrt[]{({x}^{2}+{y}^{2})} c(x,y)=\sqrt[]{({x}^{2}+{y}^{2})}](/latexrender/pictures/709211ba8dfcb6a4693deb80873bbf64.png)
...o qual
![c(x)=\sqrt[]{({x}^{2}+{(3x/(x-0.3)}^{2})} c(x)=\sqrt[]{({x}^{2}+{(3x/(x-0.3)}^{2})}](/latexrender/pictures/3018aaaacfd3727f61139ff019b32165.png)
pois obtivemos y=f(x)e
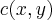
passou a ser

...agora é derivar c(x),igualar a zero e achar x,e substituir na expressao
![c(x)=\sqrt[]{({x}^{2}+{(3x/(x-0.3)}^{2})} c(x)=\sqrt[]{({x}^{2}+{(3x/(x-0.3)}^{2})}](/latexrender/pictures/3018aaaacfd3727f61139ff019b32165.png)
,entao maos a massa,resolva-a...obrigado...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Máximos e Minimos [ Derivada ]
por jazzbest » Ter Set 03, 2013 18:54
- 1 Respostas
- 2019 Exibições
- Última mensagem por young_jedi

Ter Set 03, 2013 20:28
Cálculo: Limites, Derivadas e Integrais
-
- Derivada: minimos e máximos
por Fernandobertolaccini » Dom Jul 13, 2014 23:03
- 1 Respostas
- 1716 Exibições
- Última mensagem por e8group

Seg Jul 14, 2014 01:33
Cálculo: Limites, Derivadas e Integrais
-
- Derivada: Minimos, máximos e inflexão
por Fernandobertolaccini » Dom Jul 13, 2014 15:35
- 1 Respostas
- 1590 Exibições
- Última mensagem por e8group

Dom Jul 13, 2014 16:01
Cálculo: Limites, Derivadas e Integrais
-
- Derivada: Minimos, máximos e inflexão
por Fernandobertolaccini » Dom Jul 13, 2014 15:41
- 1 Respostas
- 1300 Exibições
- Última mensagem por Russman

Dom Jul 13, 2014 16:15
Cálculo: Limites, Derivadas e Integrais
-
- dificuldade em achar derivada(máximos e mínimos)
por letciabr7 » Qua Jun 10, 2015 17:51
- 1 Respostas
- 2207 Exibições
- Última mensagem por nakagumahissao

Sáb Jun 13, 2015 13:10
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





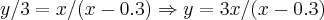 ,entao obtivemos y=f(x)...
,entao obtivemos y=f(x)...![c(x,y)=\sqrt[]{({x}^{2}+{y}^{2})} c(x,y)=\sqrt[]{({x}^{2}+{y}^{2})}](/latexrender/pictures/709211ba8dfcb6a4693deb80873bbf64.png) ...o qual
...o qual ![c(x)=\sqrt[]{({x}^{2}+{(3x/(x-0.3)}^{2})} c(x)=\sqrt[]{({x}^{2}+{(3x/(x-0.3)}^{2})}](/latexrender/pictures/3018aaaacfd3727f61139ff019b32165.png)
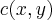 passou a ser
passou a ser  ...agora é derivar c(x),igualar a zero e achar x,e substituir na expressao
...agora é derivar c(x),igualar a zero e achar x,e substituir na expressao ![c(x)=\sqrt[]{({x}^{2}+{(3x/(x-0.3)}^{2})} c(x)=\sqrt[]{({x}^{2}+{(3x/(x-0.3)}^{2})}](/latexrender/pictures/3018aaaacfd3727f61139ff019b32165.png) ,entao maos a massa,resolva-a...obrigado...
,entao maos a massa,resolva-a...obrigado...





