 por Cleyson007 » Ter Nov 04, 2014 16:47
por Cleyson007 » Ter Nov 04, 2014 16:47
Se z = f(x,y), onde x = r² + s² e y = 2rs, encontre
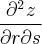
.
Alguém me esclarece da passagem grifada em vermelho?

-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Russman » Ter Nov 04, 2014 22:54
por Russman » Ter Nov 04, 2014 22:54
Primeiramente, a resolução separa as derivadas de modo que
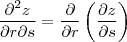
.
Mas, como
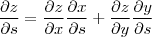
,
então
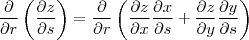
que, pela regra da soma e do produto, fica
![\frac{\partial^2 z }{\partial r \partial s} = \left (\frac{\partial x }{\partial s} \right )\left [ \frac{\partial }{\partial r} \left ( \frac{\partial z }{\partial x} \right )\right ] +\left (\frac{\partial z }{\partial x} \right )\left ( \frac{\partial^2 x }{\partial s \partial r} \rig\right ) +\left (\frac{\partial y }{\partial s} \right )\left [ \frac{\partial }{\partial r} \left ( \frac{\partial z }{\partial y} \right )\right ] +\left (\frac{\partial z }{\partial y} \right )\left ( \frac{\partial^2 y }{\partial s \partial r}\right ) \frac{\partial^2 z }{\partial r \partial s} = \left (\frac{\partial x }{\partial s} \right )\left [ \frac{\partial }{\partial r} \left ( \frac{\partial z }{\partial x} \right )\right ] +\left (\frac{\partial z }{\partial x} \right )\left ( \frac{\partial^2 x }{\partial s \partial r} \rig\right ) +\left (\frac{\partial y }{\partial s} \right )\left [ \frac{\partial }{\partial r} \left ( \frac{\partial z }{\partial y} \right )\right ] +\left (\frac{\partial z }{\partial y} \right )\left ( \frac{\partial^2 y }{\partial s \partial r}\right )](/latexrender/pictures/68244cfa76501a09e7780fa55a27c546.png)
Agora, como
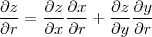
então
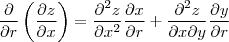
e
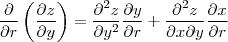
.
Portanto,
![\frac{\partial^2 z }{\partial r \partial s} = \left (\frac{\partial x }{\partial s} \right )\left [ \frac{\partial^2 z }{\partial x^2}\frac{\partial x }{\partial r}+\frac{\partial^2 z}{\partial x \partial y }\frac{\partial y}{\partial r} \right ] +\left (\frac{\partial z }{\partial x} \right )\left ( \frac{\partial^2 x }{\partial s \partial r} \rig\right ) +\left (\frac{\partial y }{\partial s} \right )\left [ \frac{\partial^2 z }{\partial y^2}\frac{\partial y }{\partial r}+\frac{\partial^2 z}{\partial x \partial y }\frac{\partial x}{\partial r}\right ] +\left (\frac{\partial z }{\partial y} \right )\left ( \frac{\partial^2 y }{\partial s \partial r}\right ) \frac{\partial^2 z }{\partial r \partial s} = \left (\frac{\partial x }{\partial s} \right )\left [ \frac{\partial^2 z }{\partial x^2}\frac{\partial x }{\partial r}+\frac{\partial^2 z}{\partial x \partial y }\frac{\partial y}{\partial r} \right ] +\left (\frac{\partial z }{\partial x} \right )\left ( \frac{\partial^2 x }{\partial s \partial r} \rig\right ) +\left (\frac{\partial y }{\partial s} \right )\left [ \frac{\partial^2 z }{\partial y^2}\frac{\partial y }{\partial r}+\frac{\partial^2 z}{\partial x \partial y }\frac{\partial x}{\partial r}\right ] +\left (\frac{\partial z }{\partial y} \right )\left ( \frac{\partial^2 y }{\partial s \partial r}\right )](/latexrender/pictures/b01a60dcac71f7bf6264e1c03d9c8a62.png)
e, enfim,
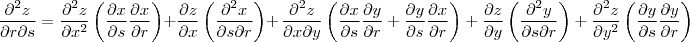
Os termos entre parenteses são calculáveis pois é dada a forma explícita das funções.
Editado pela última vez por
Russman em Qua Nov 05, 2014 01:08, em um total de 1 vez.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Cleyson007 » Ter Nov 04, 2014 23:30
por Cleyson007 » Ter Nov 04, 2014 23:30
Pode me esclarecer essa parte por favor
Russman?
Russman escreveu:que, pela regra da soma e do produto, fica
![\frac{\partial^2 z }{\partial r \partial s} = \left (\frac{\partial x }{\partial s} \right )\left [ \frac{\partial }{\partial r} \left ( \frac{\partial z }{\partial x} \right )\right ] +\left (\frac{\partial z }{\partial x} \right )\left ( \frac{\partial^2 x }{\partial s \partial r} \rig\right ) +\left (\frac{\partial y }{\partial s} \right )\left [ \frac{\partial }{\partial r} \left ( \frac{\partial z }{\partial y} \right )\right ] +\left (\frac{\partial z }{\partial y} \right )\left ( \frac{\partial^2 y }{\partial s \partial r}\right ) \frac{\partial^2 z }{\partial r \partial s} = \left (\frac{\partial x }{\partial s} \right )\left [ \frac{\partial }{\partial r} \left ( \frac{\partial z }{\partial x} \right )\right ] +\left (\frac{\partial z }{\partial x} \right )\left ( \frac{\partial^2 x }{\partial s \partial r} \rig\right ) +\left (\frac{\partial y }{\partial s} \right )\left [ \frac{\partial }{\partial r} \left ( \frac{\partial z }{\partial y} \right )\right ] +\left (\frac{\partial z }{\partial y} \right )\left ( \frac{\partial^2 y }{\partial s \partial r}\right )](/latexrender/pictures/68244cfa76501a09e7780fa55a27c546.png)
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Russman » Qua Nov 05, 2014 01:23
por Russman » Qua Nov 05, 2014 01:23
Primeiro, pela regra da soma
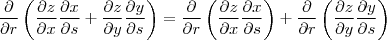
e, depois, pela regra do produto em casa parcela:
![\frac{\partial }{\partial r} \left (\frac{\partial z}{\partial x}\frac{\partial x}{\partial s}\right) = \left (\frac{\partial x}{\partial s} \right )\left [ \frac{\partial }{\partial r}\left (\frac{\partial z}{\partial x} \right ) \right ] + \left (\frac{\partial z}{\partial x} \right ) \left (\frac{\partial^2 x}{\partial r \partial s}
\right ) \frac{\partial }{\partial r} \left (\frac{\partial z}{\partial x}\frac{\partial x}{\partial s}\right) = \left (\frac{\partial x}{\partial s} \right )\left [ \frac{\partial }{\partial r}\left (\frac{\partial z}{\partial x} \right ) \right ] + \left (\frac{\partial z}{\partial x} \right ) \left (\frac{\partial^2 x}{\partial r \partial s}
\right )](/latexrender/pictures/28237eff92414e3edc406e6e9d5647ec.png)
![\frac{\partial }{\partial r} \left (\frac{\partial z}{\partial y}\frac{\partial y}{\partial s}\right) = \left (\frac{\partial y}{\partial s} \right ) \left[ \frac{\partial }{\partial r}\left (\frac{\partial z}{\partial y} \right ) \right] + \left (\frac{\partial z}{\partial y} \right ) \left (\frac{\partial^2 y}{\partial r \partial s}
\right ) \frac{\partial }{\partial r} \left (\frac{\partial z}{\partial y}\frac{\partial y}{\partial s}\right) = \left (\frac{\partial y}{\partial s} \right ) \left[ \frac{\partial }{\partial r}\left (\frac{\partial z}{\partial y} \right ) \right] + \left (\frac{\partial z}{\partial y} \right ) \left (\frac{\partial^2 y}{\partial r \partial s}
\right )](/latexrender/pictures/bdb6a87cbbbcb9f217729695edbe45c2.png)
Agora basta somar. Mais claro?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Cleyson007 » Qua Nov 05, 2014 12:39
por Cleyson007 » Qua Nov 05, 2014 12:39
Obrigado
Russman!
Agora ficou mais claro

-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [ regra da cadeia ]
por Marimar » Seg Nov 07, 2011 13:34
- 3 Respostas
- 2805 Exibições
- Última mensagem por MarceloFantini

Seg Nov 07, 2011 14:37
Cálculo: Limites, Derivadas e Integrais
-
- Regra da Cadeia
por Cleyson007 » Ter Mai 22, 2012 15:17
- 1 Respostas
- 1726 Exibições
- Última mensagem por joaofonseca

Ter Mai 22, 2012 19:14
Cálculo: Limites, Derivadas e Integrais
-
- Derivadas- regra da cadeia
por genicleide » Qua Abr 20, 2011 14:28
- 4 Respostas
- 4665 Exibições
- Última mensagem por genicleide

Qua Abr 20, 2011 19:44
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADAS] Regra da Cadeia
por pauloguerche » Qua Set 07, 2011 17:19
- 4 Respostas
- 3837 Exibições
- Última mensagem por LuizAquino

Qui Set 08, 2011 10:50
Cálculo: Limites, Derivadas e Integrais
-
- ( Regra da Cadeia ) - Cálculo II
por Marimar » Qui Nov 03, 2011 14:38
- 2 Respostas
- 2644 Exibições
- Última mensagem por LuizAquino

Dom Nov 06, 2011 12:32
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
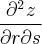 .
.


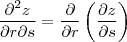 .
.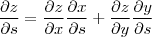 ,
,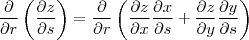
![\frac{\partial^2 z }{\partial r \partial s} = \left (\frac{\partial x }{\partial s} \right )\left [ \frac{\partial }{\partial r} \left ( \frac{\partial z }{\partial x} \right )\right ] +\left (\frac{\partial z }{\partial x} \right )\left ( \frac{\partial^2 x }{\partial s \partial r} \rig\right ) +\left (\frac{\partial y }{\partial s} \right )\left [ \frac{\partial }{\partial r} \left ( \frac{\partial z }{\partial y} \right )\right ] +\left (\frac{\partial z }{\partial y} \right )\left ( \frac{\partial^2 y }{\partial s \partial r}\right ) \frac{\partial^2 z }{\partial r \partial s} = \left (\frac{\partial x }{\partial s} \right )\left [ \frac{\partial }{\partial r} \left ( \frac{\partial z }{\partial x} \right )\right ] +\left (\frac{\partial z }{\partial x} \right )\left ( \frac{\partial^2 x }{\partial s \partial r} \rig\right ) +\left (\frac{\partial y }{\partial s} \right )\left [ \frac{\partial }{\partial r} \left ( \frac{\partial z }{\partial y} \right )\right ] +\left (\frac{\partial z }{\partial y} \right )\left ( \frac{\partial^2 y }{\partial s \partial r}\right )](/latexrender/pictures/68244cfa76501a09e7780fa55a27c546.png)
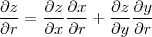
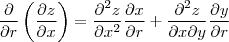
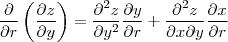 .
.![\frac{\partial^2 z }{\partial r \partial s} = \left (\frac{\partial x }{\partial s} \right )\left [ \frac{\partial^2 z }{\partial x^2}\frac{\partial x }{\partial r}+\frac{\partial^2 z}{\partial x \partial y }\frac{\partial y}{\partial r} \right ] +\left (\frac{\partial z }{\partial x} \right )\left ( \frac{\partial^2 x }{\partial s \partial r} \rig\right ) +\left (\frac{\partial y }{\partial s} \right )\left [ \frac{\partial^2 z }{\partial y^2}\frac{\partial y }{\partial r}+\frac{\partial^2 z}{\partial x \partial y }\frac{\partial x}{\partial r}\right ] +\left (\frac{\partial z }{\partial y} \right )\left ( \frac{\partial^2 y }{\partial s \partial r}\right ) \frac{\partial^2 z }{\partial r \partial s} = \left (\frac{\partial x }{\partial s} \right )\left [ \frac{\partial^2 z }{\partial x^2}\frac{\partial x }{\partial r}+\frac{\partial^2 z}{\partial x \partial y }\frac{\partial y}{\partial r} \right ] +\left (\frac{\partial z }{\partial x} \right )\left ( \frac{\partial^2 x }{\partial s \partial r} \rig\right ) +\left (\frac{\partial y }{\partial s} \right )\left [ \frac{\partial^2 z }{\partial y^2}\frac{\partial y }{\partial r}+\frac{\partial^2 z}{\partial x \partial y }\frac{\partial x}{\partial r}\right ] +\left (\frac{\partial z }{\partial y} \right )\left ( \frac{\partial^2 y }{\partial s \partial r}\right )](/latexrender/pictures/b01a60dcac71f7bf6264e1c03d9c8a62.png)
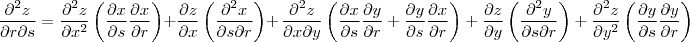


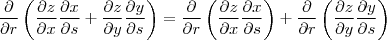
![\frac{\partial }{\partial r} \left (\frac{\partial z}{\partial x}\frac{\partial x}{\partial s}\right) = \left (\frac{\partial x}{\partial s} \right )\left [ \frac{\partial }{\partial r}\left (\frac{\partial z}{\partial x} \right ) \right ] + \left (\frac{\partial z}{\partial x} \right ) \left (\frac{\partial^2 x}{\partial r \partial s}
\right ) \frac{\partial }{\partial r} \left (\frac{\partial z}{\partial x}\frac{\partial x}{\partial s}\right) = \left (\frac{\partial x}{\partial s} \right )\left [ \frac{\partial }{\partial r}\left (\frac{\partial z}{\partial x} \right ) \right ] + \left (\frac{\partial z}{\partial x} \right ) \left (\frac{\partial^2 x}{\partial r \partial s}
\right )](/latexrender/pictures/28237eff92414e3edc406e6e9d5647ec.png)
![\frac{\partial }{\partial r} \left (\frac{\partial z}{\partial y}\frac{\partial y}{\partial s}\right) = \left (\frac{\partial y}{\partial s} \right ) \left[ \frac{\partial }{\partial r}\left (\frac{\partial z}{\partial y} \right ) \right] + \left (\frac{\partial z}{\partial y} \right ) \left (\frac{\partial^2 y}{\partial r \partial s}
\right ) \frac{\partial }{\partial r} \left (\frac{\partial z}{\partial y}\frac{\partial y}{\partial s}\right) = \left (\frac{\partial y}{\partial s} \right ) \left[ \frac{\partial }{\partial r}\left (\frac{\partial z}{\partial y} \right ) \right] + \left (\frac{\partial z}{\partial y} \right ) \left (\frac{\partial^2 y}{\partial r \partial s}
\right )](/latexrender/pictures/bdb6a87cbbbcb9f217729695edbe45c2.png)



 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
