 por Odle89 » Dom Dez 20, 2009 06:45
por Odle89 » Dom Dez 20, 2009 06:45
Bom dia pessoal!
Estou precisando de uma ajudinha pois tenho prova esta segunda e estou fazendo os exercícios de algumas provas antigas do professor porém não tenho as respostas das questões e, como ainda não estou dominando a matéria, gostaria que vocês confirmassem a resolução minha ou a corrigissem se for o caso.
tenho a função f(x) =
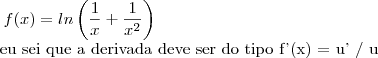
Daí fiz a função se tornar
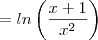
Segui então a substituição e aplicação da derivada da seguinte forma:
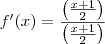
(derivada da fração superior sobre a fração inferior) e cheguei no seguinte resultado:

Está correta?
Qualquer dúvida no procedimento realizado por mim é só postar!
Abraços e desde já muito obrigado pela prontidão e parabéns ao fórum....
-
Odle89
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Dez 17, 2009 03:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: graduação eng. Civil (UFOP)
- Andamento: cursando
 por Molina » Dom Dez 20, 2009 11:29
por Molina » Dom Dez 20, 2009 11:29
Bom dia, amigo.
Já tentou resolver através da derivada composta?
Chame
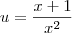
Então o que precisamos derivar é
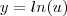
Dessa forma, para calcular
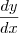
fica:
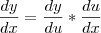
Conseguiu entender?
Estou um pouco atarefado, mas caso você não consiga eu tento resolver para você.
Abraços!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Odle89 » Dom Dez 20, 2009 17:32
por Odle89 » Dom Dez 20, 2009 17:32
molina escreveu:Bom dia, amigo.
Já tentou resolver através da derivada composta?
Chame
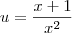
Então o que precisamos derivar é
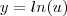
Dessa forma, para calcular
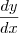
fica:
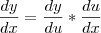
Conseguiu entender?
Estou um pouco atarefado, mas caso você não consiga eu tento resolver para você.

Boa tarde molina!
primeiramente obrigado pela atenção.
Pois foi dessa forma que eu resolvi e, pela tabela das derivadas diretas sei que a derivada de ln u = u'/u ...
O que eu tenho dúvida é se o resultado é esse pois fiz de uma outra maneira tb que acho que não é correta e obtive um resultado semelhante...
Queria saber o resultado pra poder saber a forma correta!
Obrigado novamente.
Abraços!
-
Odle89
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Dez 17, 2009 03:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: graduação eng. Civil (UFOP)
- Andamento: cursando
 por Elcioschin » Seg Dez 21, 2009 18:37
por Elcioschin » Seg Dez 21, 2009 18:37
Odle89
Tanto do seu jeito como do jeito do Molina dá certo.
Só que você cometeu um erro ao derivar:
f(x) = ln[(x + 1)/x²]
A derivada de f(x) = g(x)/h(x) é f '(x) = [h(x)*g'(x) - g(x)*h(x)]/[h(x)]² [e não f '(x) = g'(x)/h'(x)]
f '(u) = [(x²)*(x + 1)' - (x+ 1)(x²)']/(x²)² ----> f '(u) = [x²*1 - (x + 1)*(2x)]/(x²)² ----> f '(u) = (- x² - 2x)/(x²)² ----> f '(u) = - (x + 2)/x³
Agora continue:
f '(x) = u'/u -----> f '(x) = [-(x + 2)/x³]/[(x + 1)/x² ----> f '(x) = - (x + 2)/x*(x + 1)
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Molina » Seg Dez 21, 2009 23:07
por Molina » Seg Dez 21, 2009 23:07
Como eu disse, estou meio sem tempo nesse final do ano.
Então fica difícil resolver as questões, mas sempre tento ajudar da melhor forma.
Eu havia visto que a derivada estava errada, pois a integral do seu resultado nao retorna no f(x) inicial.
O Elcio já cantou a letra...
Abraços!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Cleide » Ter Dez 22, 2009 20:12
por Cleide » Ter Dez 22, 2009 20:12
Olá pessoal! Eu gostaria de saber como demonstrar que se f é uma função par, então f'(x)= -f'(-x) e também que se f é uma função ímpar, então f'(x)=f'(-x). É URGENTE!!! Obrigada...
-
Cleide
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Dez 22, 2009 20:01
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12556 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [derivada] derivada pela definição da secante
por TheKyabu » Sáb Out 27, 2012 23:24
- 2 Respostas
- 10896 Exibições
- Última mensagem por TheKyabu

Dom Out 28, 2012 11:44
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Com duas variáveis e derivada mista
por leticiaeverson » Dom Abr 22, 2018 00:39
- 3 Respostas
- 13201 Exibições
- Última mensagem por Gebe

Dom Abr 22, 2018 17:11
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada]derivada de função de raiz cúbica
por armando » Sáb Jul 20, 2013 15:22
- 4 Respostas
- 14807 Exibições
- Última mensagem por armando

Dom Jul 21, 2013 22:17
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] DERIVADA POR DEFINIÇÃO DA RAIZ DO MÓDULO DE X
por Matheusgdp » Qua Set 16, 2015 04:07
- 2 Respostas
- 5117 Exibições
- Última mensagem por Matheusgdp

Qui Set 17, 2015 18:31
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
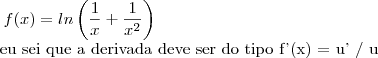
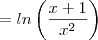
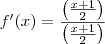 (derivada da fração superior sobre a fração inferior) e cheguei no seguinte resultado:
(derivada da fração superior sobre a fração inferior) e cheguei no seguinte resultado:


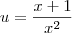
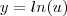
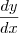 fica:
fica: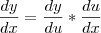



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.