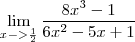
- Código: Selecionar todos
[tex][/tex]
R:6
Fico muito agradecido a quem puder ajudar!!!


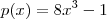 e
e 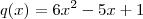 , observe que
, observe que 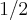 é uma raiz de q bem como de p [/tex] então podemos reescrever estes polinômios da seguinte forma :
é uma raiz de q bem como de p [/tex] então podemos reescrever estes polinômios da seguinte forma : 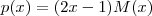 e
e 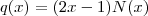 , onde
, onde 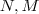 são polinômios (a ser determinador ) . Para encontrar estas funções, basta dividir
são polinômios (a ser determinador ) . Para encontrar estas funções, basta dividir 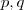 por
por 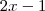 .
.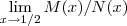 . Tente concluir .
. Tente concluir . 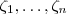 são raízes (reais ou complexas ) de um polinômio
são raízes (reais ou complexas ) de um polinômio  de grau
de grau  definido por
definido por 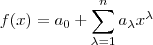 (para algumas constantes reais
(para algumas constantes reais 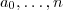 com
com  ), então é possível reescrever
), então é possível reescrever  como produto de fatores lineares do tipo
como produto de fatores lineares do tipo 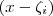 , a saber
, a saber 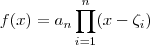 .
.
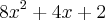
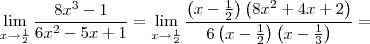
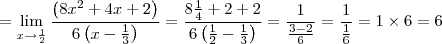


nakagumahissao escreveu:Como o denominador ficará zero quando substituirmos x por 1/2, precisaremos fatorar o denominador e o numerador
Usando bháskara e resolvendo a equação do segundo grau do denominador encontraremos x = 1/2 e x=1/3. Assim, o denominador ficará 6(x - 1/2)(x - 1/3).
Como o limite tende a 1/2, o melhor candidato para fatorarmos o numerador será (x-1/2) multiplicado por alguma coisa. Assim, dividindo o numerador por (x-1/2) obteremos:
Então teremos finalmente:

michelcosta escreveu:nakagumahissao escreveu:Como o denominador ficará zero quando substituirmos x por 1/2, precisaremos fatorar o denominador e o numerador
Usando bháskara e resolvendo a equação do segundo grau do denominador encontraremos x = 1/2 e x=1/3. Assim, o denominador ficará 6(x - 1/2)(x - 1/3).
Como o limite tende a 1/2, o melhor candidato para fatorarmos o numerador será (x-1/2) multiplicado por alguma coisa. Assim, dividindo o numerador por (x-1/2) obteremos:
Então teremos finalmente:
Muito obrigado!!!! Otima ajuda.
michelcosta escreveu:nakagumahissao escreveu:Como o denominador ficará zero quando substituirmos x por 1/2, precisaremos fatorar o denominador e o numerador
Usando bháskara e resolvendo a equação do segundo grau do denominador encontraremos x = 1/2 e x=1/3. Assim, o denominador ficará 6(x - 1/2)(x - 1/3).
Como o limite tende a 1/2, o melhor candidato para fatorarmos o numerador será (x-1/2) multiplicado por alguma coisa. Assim, dividindo o numerador por (x-1/2) obteremos:
Então teremos finalmente:
Muito obrigado!!!! Otima ajuda.

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes

 .
.
 :
: