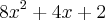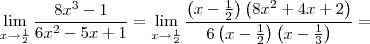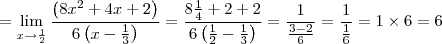por michelcosta » Dom Nov 17, 2013 10:04
por michelcosta » Dom Nov 17, 2013 10:04
lim
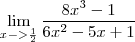
R:6
Fico muito agradecido a quem puder ajudar!!!
-
michelcosta
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Nov 17, 2013 09:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: exatas
- Andamento: cursando
 por e8group » Dom Nov 17, 2013 13:22
por e8group » Dom Nov 17, 2013 13:22
Dica :
Definamos
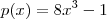
e
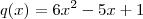
, observe que
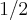
é uma raiz de q bem como de p [/tex] então podemos reescrever estes polinômios da seguinte forma :
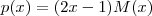
e
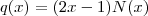
, onde
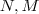
são polinômios (a ser determinador ) . Para encontrar estas funções, basta dividir
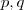
por
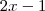
.
O limite a ser calculado então se reduz a
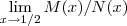
. Tente concluir .
Obs.: É sempre importante ter em mente que se
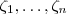
são raízes (reais ou complexas ) de um polinômio

de grau

definido por
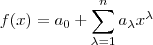
(para algumas constantes reais
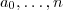
com

), então é possível reescrever

como produto de fatores lineares do tipo
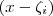
, a saber
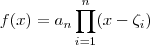
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por nakagumahissao » Dom Nov 17, 2013 13:27
por nakagumahissao » Dom Nov 17, 2013 13:27
Como o denominador ficará zero quando substituirmos x por 1/2, precisaremos fatorar o denominador e o numerador
Usando bháskara e resolvendo a equação do segundo grau do denominador encontraremos x = 1/2 e x=1/3. Assim, o denominador ficará 6(x - 1/2)(x - 1/3).
Como o limite tende a 1/2, o melhor candidato para fatorarmos o numerador será (x-1/2) multiplicado por alguma coisa. Assim, dividindo o numerador por (x-1/2) obteremos:
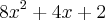
Então teremos finalmente:
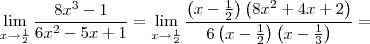
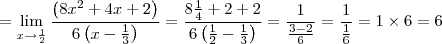

Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por michelcosta » Seg Nov 18, 2013 18:36
por michelcosta » Seg Nov 18, 2013 18:36
nakagumahissao escreveu:Como o denominador ficará zero quando substituirmos x por 1/2, precisaremos fatorar o denominador e o numerador
Usando bháskara e resolvendo a equação do segundo grau do denominador encontraremos x = 1/2 e x=1/3. Assim, o denominador ficará 6(x - 1/2)(x - 1/3).
Como o limite tende a 1/2, o melhor candidato para fatorarmos o numerador será (x-1/2) multiplicado por alguma coisa. Assim, dividindo o numerador por (x-1/2) obteremos:
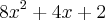
Então teremos finalmente:
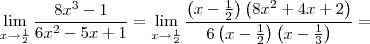

Muito obrigado!!!! Otima ajuda.
-
michelcosta
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Nov 17, 2013 09:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: exatas
- Andamento: cursando
 por michelcosta » Seg Nov 18, 2013 18:37
por michelcosta » Seg Nov 18, 2013 18:37
michelcosta escreveu:nakagumahissao escreveu:Como o denominador ficará zero quando substituirmos x por 1/2, precisaremos fatorar o denominador e o numerador
Usando bháskara e resolvendo a equação do segundo grau do denominador encontraremos x = 1/2 e x=1/3. Assim, o denominador ficará 6(x - 1/2)(x - 1/3).
Como o limite tende a 1/2, o melhor candidato para fatorarmos o numerador será (x-1/2) multiplicado por alguma coisa. Assim, dividindo o numerador por (x-1/2) obteremos:
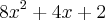
Então teremos finalmente:
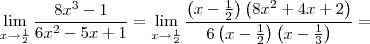

Muito obrigado!!!! Otima ajuda.
michelcosta escreveu:nakagumahissao escreveu:Como o denominador ficará zero quando substituirmos x por 1/2, precisaremos fatorar o denominador e o numerador
Usando bháskara e resolvendo a equação do segundo grau do denominador encontraremos x = 1/2 e x=1/3. Assim, o denominador ficará 6(x - 1/2)(x - 1/3).
Como o limite tende a 1/2, o melhor candidato para fatorarmos o numerador será (x-1/2) multiplicado por alguma coisa. Assim, dividindo o numerador por (x-1/2) obteremos:
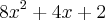
Então teremos finalmente:
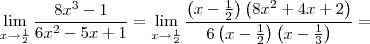
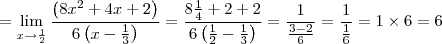

Muito obrigado!!!! Otima ajuda.
Perfeita explicação ajudou muito mesmo, muitíssimo obrigado.
-
michelcosta
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Nov 17, 2013 09:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: exatas
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6650 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4796 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5127 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7270 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4446 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
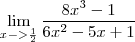


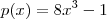 e
e 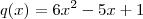 , observe que
, observe que 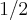 é uma raiz de q bem como de p [/tex] então podemos reescrever estes polinômios da seguinte forma :
é uma raiz de q bem como de p [/tex] então podemos reescrever estes polinômios da seguinte forma : 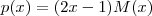 e
e 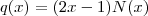 , onde
, onde 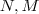 são polinômios (a ser determinador ) . Para encontrar estas funções, basta dividir
são polinômios (a ser determinador ) . Para encontrar estas funções, basta dividir 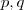 por
por 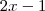 .
.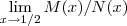 . Tente concluir .
. Tente concluir . 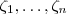 são raízes (reais ou complexas ) de um polinômio
são raízes (reais ou complexas ) de um polinômio  de grau
de grau  definido por
definido por 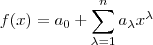 (para algumas constantes reais
(para algumas constantes reais 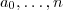 com
com  ), então é possível reescrever
), então é possível reescrever  como produto de fatores lineares do tipo
como produto de fatores lineares do tipo 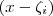 , a saber
, a saber 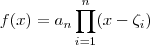 .
.