 por Lenin » Qua Set 25, 2013 21:21
por Lenin » Qua Set 25, 2013 21:21
pessoal, tenho dúvida em uma questão de limites.
Para cada função f a seguir, determine D(f) e, se possível, a função g: R->R, tal que g é contínua e g(x) = f(x), para todo x pertencente D(x):
a)
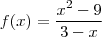
eu fiz da seguinte forma: como ele fala que g(x)=f(x) eu fui usando o f(x), e acho que estou errado nessa parte. Logo eu fiz o seguinte.
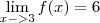
porém o f(3) não está definido..quando eu faço dá uma indeterminação (não sei se para este caso tem que tirar a indeterminação) porém, sou leigo em calculo, comecei agora. Eu queria entender essa questão, desde já agradeço..preciso muito dessa questão até amanhã..se alguem puder muito me ajudar..obrigado
-
Lenin
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Abr 10, 2013 23:08
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Cursinho
- Andamento: cursando
 por Man Utd » Qua Set 25, 2013 21:35
por Man Utd » Qua Set 25, 2013 21:35
Lenin escreveu:pessoal, tenho dúvida em uma questão de limites.
Para cada função f a seguir, determine D(f) e, se possível, a função g: R->R, tal que g é contínua e g(x) = f(x), para todo x pertencente D(x):
a)
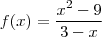
eu fiz da seguinte forma: como ele fala que g(x)=f(x) eu fui usando o f(x), e acho que estou errado nessa parte. Logo eu fiz o seguinte.
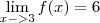
porém o f(3) não está definido..quando eu faço dá uma indeterminação (não sei se para este caso tem que tirar a indeterminação) porém, sou leigo em calculo, comecei agora. Eu queria entender essa questão, desde já agradeço..preciso muito dessa questão até amanhã..se alguem puder muito me ajudar..obrigado
olá

não tenho muita certeza,mas vamos lá

:
o dominio de f será
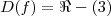
que é o conjunto dos números reais exceto 3 que zeraria o denominador,já para obter uma função g(x) contínua e g(x) = f(x), para todo x pertencente ao dominio de f(x) :
vamos fatorar para tirar a indeterminação:
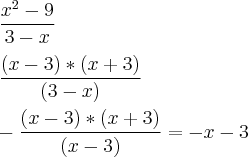
que para todo x pertecente ao dominio de f,a função possui a msm imagem e é continua.
espero que seja isso.
att mais

-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Continuidade de função
por marinalcd » Qui Ago 23, 2012 20:52
- 0 Respostas
- 1052 Exibições
- Última mensagem por marinalcd

Qui Ago 23, 2012 20:52
Funções
-
- continuidade da função
por Sherminator » Sex Nov 16, 2012 13:13
- 15 Respostas
- 12191 Exibições
- Última mensagem por Sherminator

Ter Nov 20, 2012 12:55
Cálculo: Limites, Derivadas e Integrais
-
- Estudo da [continuidade] de uma função
por Teh_eng » Qui Mai 03, 2012 13:43
- 1 Respostas
- 1381 Exibições
- Última mensagem por Russman

Qui Mai 03, 2012 14:52
Cálculo: Limites, Derivadas e Integrais
-
- [Continuidade de função] Demonstração
por Gustavo Gomes » Qui Nov 08, 2012 21:41
- 2 Respostas
- 1601 Exibições
- Última mensagem por Gustavo Gomes

Sex Nov 09, 2012 21:33
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Continuidade - Função
por raimundoocjr » Ter Mai 07, 2013 20:16
- 1 Respostas
- 1255 Exibições
- Última mensagem por e8group

Ter Mai 07, 2013 21:16
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
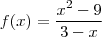
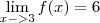



 :
: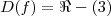 que é o conjunto dos números reais exceto 3 que zeraria o denominador,já para obter uma função g(x) contínua e g(x) = f(x), para todo x pertencente ao dominio de f(x) :
que é o conjunto dos números reais exceto 3 que zeraria o denominador,já para obter uma função g(x) contínua e g(x) = f(x), para todo x pertencente ao dominio de f(x) :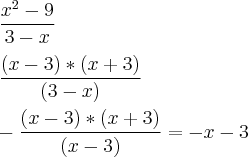



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.