Então estou em duvida nesse exercicio.
-- Calcular a derivada
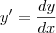 da seguinte função definida na forma paramétrica. Para quais valores de t, y' está definida?
da seguinte função definida na forma paramétrica. Para quais valores de t, y' está definida?Essa é a função dada na forma paramétrica:
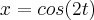
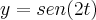
e isso para
![t\in\left[0,\frac{\pi}{2} \right] t\in\left[0,\frac{\pi}{2} \right]](/latexrender/pictures/89655ed5c73f7cdac67dc885da565d3c.png)
Calculei a derivada e deu:
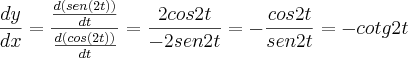
A minha duvida é nessa questão, como é que vou colocar
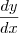 em função de x?
em função de x?e mesmo se eu conseguir colocar, para quais valores de t, y' está definida, sendo que coloquei
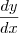 em função de x?
em função de x?

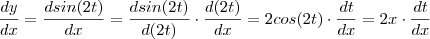 .
.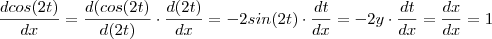 .
.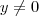 podemos isolar
podemos isolar 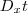 ,
,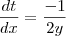 .
. 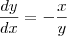 (Que é o que vc achou).
(Que é o que vc achou).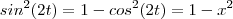 .E como ,
.E como , 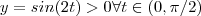 ,
, 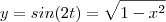 .
. 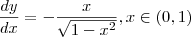 .
. ![[0,\pi/2] [0,\pi/2]](/latexrender/pictures/6b59bc315c28725e04e9331e71527914.png) há dois valores que
há dois valores que 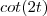 não está definido .
não está definido .
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)