uma companhia possui trés fabricas produzindo o mesmo produto. se as fabricas A,B e C produzem x, y e z unidades respectivas, seus custos de fabricação são (3x²+200), (y²+400) e (2z²+300).
Se um pedido de 1.100 unidades dever ser entregue, use o método dos multiplicadores de lagrange para determinar como a produção dever ser distribuidora entre as trés fabricas, a fim de minimizar o custo total da fabricação.


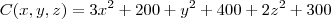
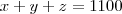
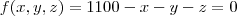
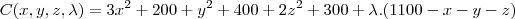
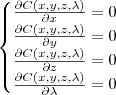


 .
.
 :
: