Eu não tou conseguindo derivar essa função:
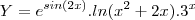
Eu pensei na Regra da Cadeia, mas não sei se posso aplicá-la...

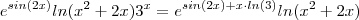 pois
pois 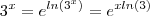 .Utilizando a propriedade
.Utilizando a propriedade  chega-se na igualdade .
chega-se na igualdade .
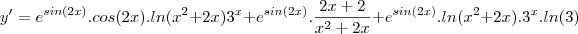
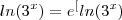 então minha resposta deu assim:
então minha resposta deu assim: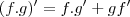

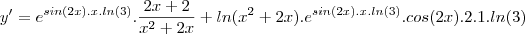

 digitou
digitou 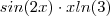 .Para chegar no gabarito , basta notar que
.Para chegar no gabarito , basta notar que 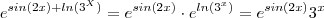 .
.  definida por
definida por 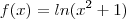 .
. 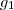 e
e 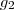 . Onde :
. Onde :  ;
; 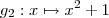 .
. 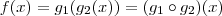 .
. 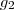 é estar contida no domínio da função
é estar contida no domínio da função 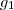 . Isto significa que o domínio da função
. Isto significa que o domínio da função 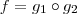 será o da
será o da 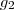 . Estou deixando isto claro porque nem sempre isto ocorrerá . Mas ,lembre-se , dada função composta
. Estou deixando isto claro porque nem sempre isto ocorrerá . Mas ,lembre-se , dada função composta  temos
temos 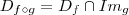 .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes

 .
.
 :
: