 por fabriel » Sex Set 21, 2012 22:56
por fabriel » Sex Set 21, 2012 22:56
Por favor me ajudem de onde eu pareai nessa questão, eu empaquei no estudo do sinal.:
#Estude a função
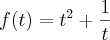
com relação à concavidade e pontos de inflexão.
Calculando a 1° derivada:
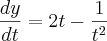
Calculando a 2° derivada:
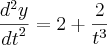
Para achar as raízes:
![2 + \frac{2}{{t}^{3}} = 0 \Leftrightarrow t = \sqrt[3]{-1} = -1 2 + \frac{2}{{t}^{3}} = 0 \Leftrightarrow t = \sqrt[3]{-1} = -1](/latexrender/pictures/deff47efd7c02adcb4ed33ca403394a6.png)
Então me ajude a partir daí por favor, to no caminho certo??
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por MarceloFantini » Sex Set 21, 2012 23:47
por MarceloFantini » Sex Set 21, 2012 23:47
Sim, você já encontrou o ponto de inflexão. Falta encontrar os intervalos em que a derivada é maior ou menor que zero.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por fabriel » Sáb Set 22, 2012 01:07
por fabriel » Sáb Set 22, 2012 01:07
Obrigado
Fiz o estudo do sinal:
Conc. p/ cima em ]-

, -1[ e ]0,+

[
Conc. p/ baixo em ]-1,0[
será que é isso??
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por MarceloFantini » Sáb Set 22, 2012 01:18
por MarceloFantini » Sáb Set 22, 2012 01:18
Sim, está tudo correto.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Achar pontos de inflexão
por alienpuke » Qui Nov 12, 2015 11:31
- 2 Respostas
- 3781 Exibições
- Última mensagem por alienpuke

Ter Nov 17, 2015 10:01
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo I] Concavidade - Ponto de Inflexão
por Pessoa Estranha » Ter Nov 18, 2014 00:38
- 3 Respostas
- 2412 Exibições
- Última mensagem por adauto martins

Sex Nov 21, 2014 17:01
Cálculo: Limites, Derivadas e Integrais
-
- Número de pontos de inflexão da seguinte função
por OtavioBonassi » Sáb Jul 16, 2011 14:54
- 1 Respostas
- 1484 Exibições
- Última mensagem por LuizAquino

Sáb Jul 16, 2011 18:04
Cálculo: Limites, Derivadas e Integrais
-
- [calculo]concavidade pela derivada
por beel » Dom Nov 06, 2011 17:40
- 1 Respostas
- 1363 Exibições
- Última mensagem por LuizAquino

Qua Nov 09, 2011 08:54
Cálculo: Limites, Derivadas e Integrais
-
- [derivada] Ponto minimo/máximo e concavidade
por gabriel feron » Dom Out 07, 2012 03:52
- 1 Respostas
- 2204 Exibições
- Última mensagem por young_jedi

Dom Out 07, 2012 10:56
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
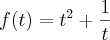 com relação à concavidade e pontos de inflexão.
com relação à concavidade e pontos de inflexão.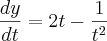
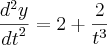
![2 + \frac{2}{{t}^{3}} = 0 \Leftrightarrow t = \sqrt[3]{-1} = -1 2 + \frac{2}{{t}^{3}} = 0 \Leftrightarrow t = \sqrt[3]{-1} = -1](/latexrender/pictures/deff47efd7c02adcb4ed33ca403394a6.png)

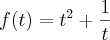 com relação à concavidade e pontos de inflexão.
com relação à concavidade e pontos de inflexão.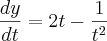
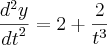
![2 + \frac{2}{{t}^{3}} = 0 \Leftrightarrow t = \sqrt[3]{-1} = -1 2 + \frac{2}{{t}^{3}} = 0 \Leftrightarrow t = \sqrt[3]{-1} = -1](/latexrender/pictures/deff47efd7c02adcb4ed33ca403394a6.png)



 , -1[ e ]0,+
, -1[ e ]0,+ [
[

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.