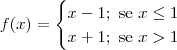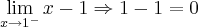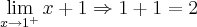por Claudin » Sáb Mai 28, 2011 10:26
por Claudin » Sáb Mai 28, 2011 10:26
Pode-se afirmar que todas as vezes que existir limites laterais diferentes o limite não existe?
Ou seja, sempre que for uma função descontínua não terá limites (no caso somente os limites laterais diferentes).
Abraço
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Sáb Mai 28, 2011 19:38
por LuizAquino » Sáb Mai 28, 2011 19:38
Por
definição, dizemos que
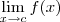
existe e é igual a
L se, e somente se,
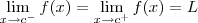
.
Não confundir o fato de uma função ser descontínua em um ponto com o fato de existir ou não limite naquele ponto.
Por exemplo, a função
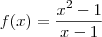
é descontínua no ponto x = 1, porém
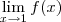
existe e é igual a 2.
Já a função
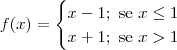
também é descontínua no ponto x = 1 e temos que
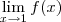
não existe.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Dom Mai 29, 2011 01:42
por Claudin » Dom Mai 29, 2011 01:42
Valeu pela ajuda Luiz.
No ultimo exemplo, consegui notar a descontinuidade. Porém não consegui notar que o limite não existe, quando x tende a 1. Não seria 0 a resposta para o limite?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Dom Mai 29, 2011 09:52
por LuizAquino » Dom Mai 29, 2011 09:52
Qual é o valor de
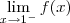
?
E de
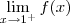
?
Os valores desses limites laterais são iguais?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Dom Mai 29, 2011 20:41
por Claudin » Dom Mai 29, 2011 20:41
LuizAquino escreveu:Qual é o valor de
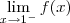
?
E de
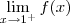
?
Os valores desses limites laterais são iguais?
No segundo exemplo como ja tinha dito, a
descontinuidade foi entendida.
Onde:
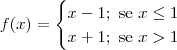
Portanto:
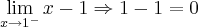
e
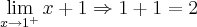
Concluindo que os limites laterais são distintos, comprovando a descontinuidade!
Gostaria de saber porque não existe o limite?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Dom Mai 29, 2011 21:09
por LuizAquino » Dom Mai 29, 2011 21:09
Claudin escreveu:Gostaria de saber porque não existe o limite?
Leia com atenção a
definição dada acima.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Dom Mai 29, 2011 21:11
por Claudin » Dom Mai 29, 2011 21:11
Li novamente, e acabei de entender Luiz
muito obrigado
Abraço
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6650 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4796 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5128 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7270 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4446 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



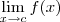 existe e é igual a L se, e somente se,
existe e é igual a L se, e somente se, 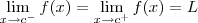 .
.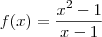 é descontínua no ponto x = 1, porém
é descontínua no ponto x = 1, porém 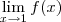 existe e é igual a 2.
existe e é igual a 2.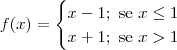 também é descontínua no ponto x = 1 e temos que
também é descontínua no ponto x = 1 e temos que 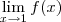 não existe.
não existe.

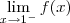 ?
?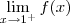 ?
?
?
?