 por AlbertoAM » Sex Abr 15, 2011 23:28
por AlbertoAM » Sex Abr 15, 2011 23:28
Olá, estou com dificuldade nesse exercício, onde ele pede para derivar e simplificar:
![f(x)=\frac{3}{5}x\sqrt[3]{x^2}+\frac{3}{2}x\sqrt[3]{x}+x f(x)=\frac{3}{5}x\sqrt[3]{x^2}+\frac{3}{2}x\sqrt[3]{x}+x](/latexrender/pictures/9ba236e43230f07d8d593ec26db39252.png)
R.:
![f'(x)=(\sqrt[3]{x}+1)^2 f'(x)=(\sqrt[3]{x}+1)^2](/latexrender/pictures/fd9f3539665ac07853181db059988911.png)
Então, nesse exercício teríamos que primeiro utilizar a álgebra das derivadas e depois usar a "tabela de derivadas".Eu pensei em separar assim:
![f'(x)=x'\:(\frac{3}{5}\sqrt[3]{{x}^{2}})'+x'(\frac{3}{2}\sqrt[3]{x})+x' f'(x)=x'\:(\frac{3}{5}\sqrt[3]{{x}^{2}})'+x'(\frac{3}{2}\sqrt[3]{x})+x'](/latexrender/pictures/57ceff89c0483737f5d2eb5ce13692b5.png)
Só que se eu fizesse isso eu poderia fazer isso também:
![f'(x)=\frac{3}{5}'\:(x\sqrt[3]{{x}^{2}})'... f'(x)=\frac{3}{5}'\:(x\sqrt[3]{{x}^{2}})'...](/latexrender/pictures/93e3467338157842fd9558fe9c270a06.png)
Ai a derivada daria zero.Então deve estar errada a minha idéia.Eu teria que usar que tipo de técnica para derivar essa função?
Outras dúvida, eu queria saber se para derivar uma função usando a definição, tanto faz eu usar esse limite
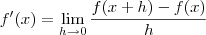
ou esse
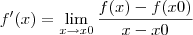
, ou seja, eles são equivalentes, vão dar a mesma derivada?
Sem querer abusar, poderia verificar se eu resolvi corretamente esse exercício, onde ele pede para derivar e simplificar:
http://img13.imageshack.us/i/derivada.png/Muito obrigado.
-
AlbertoAM
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Qui Nov 11, 2010 15:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por AlbertoAM » Sáb Abr 16, 2011 01:36
por AlbertoAM » Sáb Abr 16, 2011 01:36
Muito Obrigado pela ajuda.
-
AlbertoAM
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Qui Nov 11, 2010 15:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivadas] Dificuldade para calcular derivadas CDI 1
por srmai » Seg Nov 04, 2013 01:21
- 0 Respostas
- 2265 Exibições
- Última mensagem por srmai

Seg Nov 04, 2013 01:21
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Interpretação de derivadas e funções
por vinik1 » Qua Out 12, 2011 16:03
- 5 Respostas
- 7486 Exibições
- Última mensagem por vinik1

Qui Out 13, 2011 10:48
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Derivadas em pontos dados
por MarlonMO250 » Sex Mar 01, 2013 21:02
- 6 Respostas
- 4965 Exibições
- Última mensagem por Russman

Sáb Mar 02, 2013 03:42
Cálculo: Limites, Derivadas e Integrais
-
- (derivadas) derivadas com raiz como se faz
por jana garcia » Qua Jun 25, 2014 00:28
- 1 Respostas
- 2974 Exibições
- Última mensagem por e8group

Qua Jun 25, 2014 01:13
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Derivadas com definição de limites
 por concurseironf » Sex Set 05, 2014 18:11
por concurseironf » Sex Set 05, 2014 18:11
- 1 Respostas
- 1999 Exibições
- Última mensagem por DanielFerreira

Dom Set 07, 2014 22:18
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![f(x)=\frac{3}{5}x\sqrt[3]{x^2}+\frac{3}{2}x\sqrt[3]{x}+x f(x)=\frac{3}{5}x\sqrt[3]{x^2}+\frac{3}{2}x\sqrt[3]{x}+x](/latexrender/pictures/9ba236e43230f07d8d593ec26db39252.png)
![f'(x)=(\sqrt[3]{x}+1)^2 f'(x)=(\sqrt[3]{x}+1)^2](/latexrender/pictures/fd9f3539665ac07853181db059988911.png)
![f'(x)=x'\:(\frac{3}{5}\sqrt[3]{{x}^{2}})'+x'(\frac{3}{2}\sqrt[3]{x})+x' f'(x)=x'\:(\frac{3}{5}\sqrt[3]{{x}^{2}})'+x'(\frac{3}{2}\sqrt[3]{x})+x'](/latexrender/pictures/57ceff89c0483737f5d2eb5ce13692b5.png)
![f'(x)=\frac{3}{5}'\:(x\sqrt[3]{{x}^{2}})'... f'(x)=\frac{3}{5}'\:(x\sqrt[3]{{x}^{2}})'...](/latexrender/pictures/93e3467338157842fd9558fe9c270a06.png)
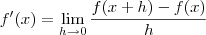 ou esse
ou esse 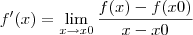 , ou seja, eles são equivalentes, vão dar a mesma derivada?
, ou seja, eles são equivalentes, vão dar a mesma derivada?

![x \sqrt[3]{x^2} = x \cdot x^{\frac{2}{3}} = x^{\frac{5}{3}} x \sqrt[3]{x^2} = x \cdot x^{\frac{2}{3}} = x^{\frac{5}{3}}](/latexrender/pictures/248f4455db68774e5c2344031444614c.png)
![x\sqrt[3]{x} = x \cdot x^{\frac{1}{3}} = x^{\frac{4}{3}} x\sqrt[3]{x} = x \cdot x^{\frac{1}{3}} = x^{\frac{4}{3}}](/latexrender/pictures/888e939381febca0e459210039bd7712.png)
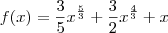
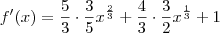
![\therefore f'(x) = x^{\frac{2}{3}} + 2 x^{\frac{1}{3}} + 1 = (x^{\frac{1}{3}} + 1)^2 = (\sqrt[3]{x} +1)^2 \therefore f'(x) = x^{\frac{2}{3}} + 2 x^{\frac{1}{3}} + 1 = (x^{\frac{1}{3}} + 1)^2 = (\sqrt[3]{x} +1)^2](/latexrender/pictures/30a4d4fb0a93882e85fa18703fef53ff.png)







