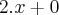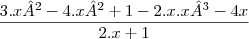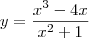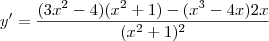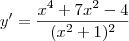por Tayron » Qua Fev 09, 2011 16:35
por Tayron » Qua Fev 09, 2011 16:35
Bom em primeiro lugar Ótimo site de estudos, estão de parabéns já consegui tirar varias duvidas que tinha somente com visitas, mas hoje estou com um probleminha um pouco maior, trata - se de uma duvida em um problema de Derivada do Quociente onde sempre me perco no meio da resolução, vamos ao problema.
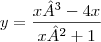
Resolvi ele até certa parte:
u =
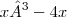
u' =

v =
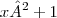
v' =
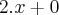
y' =
u'.v-v'.u v²
y' =
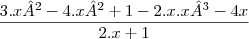
Bom ai eu me perco não sei se o processo até ai está 100% correto mais foi assim que consegui assimilar quando o professor explicou.
* Desculpem não consegui colocar o símbolo de derivado no "u e v" apresentado na formula.
** Coloquei as variáveis u e v para definirem a formula antes de derivada e depois de derivar.
*** Preciso de ajuda em como proceder pois tenho uma grande dificuldade pois não sei se devo multiplicar a primeira pela segunda parte.
Grato!
-
Tayron
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Fev 09, 2011 15:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng.Cívil
- Andamento: cursando
 por LuizAquino » Qua Fev 09, 2011 17:15
por LuizAquino » Qua Fev 09, 2011 17:15
Olá Tayron,
Primeiro, gostaria de lhe dizer que para escrever x elevado a n, basta usar o código LaTeX x^n. Além disso, para colocar o símbolo de derivada em u, por exemplo, use o comando LaTeX u^\prime.
Dito isso, a sua dúvida é a derivada de:
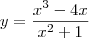
Usando a regra do quociente, temos que:

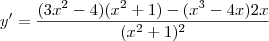
Aplicando a distributiva e simplificando os termos, obtemos:
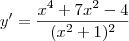
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12556 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- Derivada do Quociente
 por dekol2 » Dom Mai 06, 2012 20:39
por dekol2 » Dom Mai 06, 2012 20:39
- 4 Respostas
- 4295 Exibições
- Última mensagem por LuizAquino

Seg Mai 07, 2012 11:34
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Quociente
por Paraujo » Dom Set 23, 2012 21:15
- 9 Respostas
- 6597 Exibições
- Última mensagem por Paraujo

Ter Set 25, 2012 12:15
Cálculo: Limites, Derivadas e Integrais
-
- Derivada quociente.
por Sobreira » Seg Out 29, 2012 16:24
- 3 Respostas
- 2909 Exibições
- Última mensagem por young_jedi

Seg Out 29, 2012 17:58
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida com derivada do quociente
por arnoanderson » Seg Nov 02, 2009 12:08
- 2 Respostas
- 3864 Exibições
- Última mensagem por arnoanderson

Ter Nov 03, 2009 09:36
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
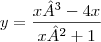
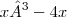 u' =
u' = 
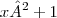 v' =
v' =