Dada
![f (x) =\sqrt[3]{\frac{x}{x^3+1}} f (x) =\sqrt[3]{\frac{x}{x^3+1}}](/latexrender/pictures/caf5f00aa2714bc63966e8f65ca25765.png)
Calcule a f´(x)
Incialmente eu transformei a fração em produto porque é bem mais prático usar a regra do produto ao invés da do quociente.
Logo,
![f (x) =\sqrt[3]{\frac{x}{x^3+1}} = {x}^{1/3}{(x^3+1)}^{-1/3} f (x) =\sqrt[3]{\frac{x}{x^3+1}} = {x}^{1/3}{(x^3+1)}^{-1/3}](/latexrender/pictures/73f3b61c728598539edefde0aff5a617.png)
Combinado a regra do produto com a regra da cadeia, obtemos:
Aplicando a regra do produto, temos:
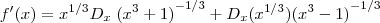
Aplicando a regra da cadeia, temos:
![f'(x) = {x}^{1/3}[\frac{-1}{3}{(x^3+1)}^{-4/3}(3x^2)] + [ \frac{1}{3}{x}^{-2/3}]{(x^3+1)}^{-1/3} f'(x) = {x}^{1/3}[\frac{-1}{3}{(x^3+1)}^{-4/3}(3x^2)] + [ \frac{1}{3}{x}^{-2/3}]{(x^3+1)}^{-1/3}](/latexrender/pictures/6f26960fc090bf7c8da9379408b8d4b4.png)
Meu professor disse que até aí esta correto, basta agora colocar algum termo em evidência para obter
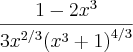
Mas não estou conseguindo.
Favor explicar detalhadamente


![f(x) = \sqrt[3]{\frac{x}{x^3+1}} f(x) = \sqrt[3]{\frac{x}{x^3+1}}](/latexrender/pictures/403c0ca76f7c11ad98441e3cdf0ea7ce.png)
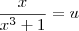 temos:
temos:![\frac{d u^{2/3}}{du} \Rightarrow \, \frac{1}{3 \cdot \sqrt [3] {u^2}} \cdot u` \frac{d u^{2/3}}{du} \Rightarrow \, \frac{1}{3 \cdot \sqrt [3] {u^2}} \cdot u`](/latexrender/pictures/c34568fbf96ee459c54b1ca515dfbb85.png)
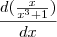
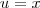 e
e 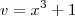 teremos:
teremos: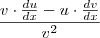

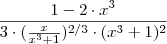
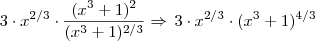
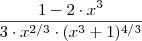


 .
.
 :
: