Bom dia.
Bem, sendo o triângulo retângulo,a resolução é fácil.
1º ponto: como os lados AC e AB =1, temos um triângulo isósceles.
Sabemos que a soma dos ângulos internos de um triângulo é sempre igual a 180º. Ora, como temos um triângulo isósceles, o ângulo em C será igual ao ângulo em B. Designando por

, temos que
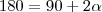
. Logo

º.
Centremo-nos agora no triângulo ADB. Ora, vamos dividir este triângulo em D, através de uma perpendicular, fazendo com que tenhamos 2 triângulos retângulos: ADE e DEB (onde E é um novo ponto que resulta da perpendicular em D até à aresta AB).
Designemos por

o ângulo em A, relativamente ao triângulo ADB. Ora

=180-45-120=15.
Designemos por y a distância DE e por x a distância EB.Logo, AE= 1-x.
Sendo assim, podemos aplicar razões trigonométricas aos 2 novos triângulos retângulos, formando um sistema:
tg(15)=
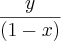
e tg(45)=

.
Resolvendo este sistema, vamos ter y
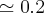
.
Sabendo y, podemos agora achar AD, que não é mais do que a hipótenusa do triângulo de ADE, através do seno: AD
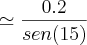
.
(Usei arredondamentos a uma casa decimal).
Espero que ajude.








 , temos que
, temos que 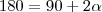 . Logo
. Logo  º.
º. o ângulo em A, relativamente ao triângulo ADB. Ora
o ângulo em A, relativamente ao triângulo ADB. Ora  =180-45-120=15.
=180-45-120=15.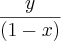 e tg(45)=
e tg(45)= .
.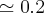 .
.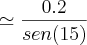 .
.
