 por adauto martins » Seg Set 30, 2019 14:28
por adauto martins » Seg Set 30, 2019 14:28
(ita-instituto tecnologico da aeronautica-exame de admissao 1953)
partindo de um quadrado
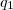
,cujo lado mede a metros,considere os quarados

tais que os vertices de cada quadrado sejam os pontos medios
do quadrado anterior.calcular entao,as somas das areas dos quadrados

.
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Seg Out 07, 2019 18:04
por adauto martins » Seg Out 07, 2019 18:04
soluçao:
vamos tomar o lado de
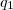
de

o segundo quadrado

,q.tera sua medida na metade do lado de
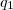
tera entao lado
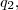
![{l}_{2}=l \sqrt[]{2}/2\Rightarrow {A}_{{q}_{2}}={l}^{2}/2 {l}_{2}=l \sqrt[]{2}/2\Rightarrow {A}_{{q}_{2}}={l}^{2}/2](/latexrender/pictures/fcdac5b906ad72ac8cfbc78d6d45064e.png)
analogamente

,
![{l}_{3}=l\sqrt[]{2}/4\Rightarrow {A}_{{q}_{3}}={l}^{2}/4 {l}_{3}=l\sqrt[]{2}/4\Rightarrow {A}_{{q}_{3}}={l}^{2}/4](/latexrender/pictures/b7832a29f6cc6048ad43d35870ef6eb9.png)
...e assim,sucessivamente,logo a soma S,sera:

-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Qui Out 17, 2019 14:01
por adauto martins » Qui Out 17, 2019 14:01
a soluçao apresentada dessa questao esta incorreta,pois as somas areas é finita,e eu usei para somas infinitas.
qdo eu tiver a soluçao correta,posto-a.se alguem souber a soluçao por favor,poste-a...
obrigado,adauto martins
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Sex Out 25, 2019 18:05
por adauto martins » Sex Out 25, 2019 18:05
correçao:
como disse anteriormente essa soma é finita,se consideramos a soma infinita a soluçao apresentada é correta,o raciocinio é o mesmo.entao vamos a soluçao correta dessa questao:
chegamos a soma:

-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- exerc.proposto
por adauto martins » Seg Set 16, 2019 15:41
- 1 Respostas
- 12337 Exibições
- Última mensagem por DanielFerreira

Ter Set 17, 2019 12:53
Equações
-
- exerc.proposto
por adauto martins » Seg Set 16, 2019 15:51
- 1 Respostas
- 12632 Exibições
- Última mensagem por DanielFerreira

Ter Set 17, 2019 12:45
Polinômios
-
- exerc.proposto
por adauto martins » Seg Set 16, 2019 16:02
- 1 Respostas
- 4919 Exibições
- Última mensagem por adauto martins

Qui Set 19, 2019 09:39
Equações
-
- exerc.proposto
por adauto martins » Seg Set 16, 2019 16:09
- 4 Respostas
- 8705 Exibições
- Última mensagem por adauto martins

Sex Out 11, 2019 10:34
Números Complexos
-
- exerc.proposto
por adauto martins » Ter Set 17, 2019 10:30
- 1 Respostas
- 4215 Exibições
- Última mensagem por adauto martins

Seg Set 23, 2019 23:57
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
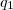 ,cujo lado mede a metros,considere os quarados
,cujo lado mede a metros,considere os quarados  tais que os vertices de cada quadrado sejam os pontos medios
tais que os vertices de cada quadrado sejam os pontos medios .
.
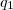 ,cujo lado mede a metros,considere os quarados
,cujo lado mede a metros,considere os quarados  tais que os vertices de cada quadrado sejam os pontos medios
tais que os vertices de cada quadrado sejam os pontos medios .
.
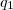 de
de 
 ,q.tera sua medida na metade do lado de
,q.tera sua medida na metade do lado de 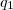
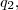
![{l}_{2}=l \sqrt[]{2}/2\Rightarrow {A}_{{q}_{2}}={l}^{2}/2 {l}_{2}=l \sqrt[]{2}/2\Rightarrow {A}_{{q}_{2}}={l}^{2}/2](/latexrender/pictures/fcdac5b906ad72ac8cfbc78d6d45064e.png)
 ,
,![{l}_{3}=l\sqrt[]{2}/4\Rightarrow {A}_{{q}_{3}}={l}^{2}/4 {l}_{3}=l\sqrt[]{2}/4\Rightarrow {A}_{{q}_{3}}={l}^{2}/4](/latexrender/pictures/b7832a29f6cc6048ad43d35870ef6eb9.png)




