por rafaelcb » Qui Set 30, 2010 13:05
Bom Dia,
Meu nome é Rafael, e eu não estou conseguindo resolver esse exercício de Geometria, se alguem puder me ajudar eu ficaria muito grato.
Muito Obrigado pela atenção e paciência
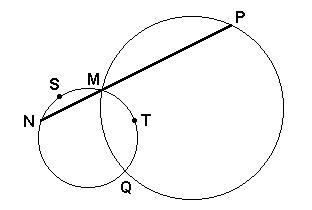
(Mack 98) Na figura a seguir, os arcos QMP e MTQ medem, respectivamente, 170° e 130°. Então, o arco MSN mede:
a) 60ºb) 70º
c) 80º
d) 100º
e) 110º
- Mack 98.JPG (7.73 KiB) Exibido 4686 vezes
-
rafaelcb
- Novo Usuário
-
- Mensagens: 2
- Registrado em: Qui Set 30, 2010 12:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Psicologia
- Andamento: formado
por Douglasm » Qui Set 30, 2010 18:20
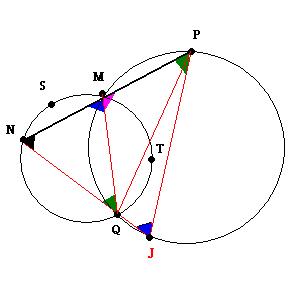
Na verdade tudo de que precisa é uma construção conveniente. Como já é bastante claro o desenho, só vou indicar os ângulos:
Preto: 65º
Azul: 85º
Verde: 30º (resposta)
Rosa: 95º
Note que o ângulo que descreve um arco na borda da circunferência, vale metade do ângulo que descreve o mesmo arco a partir do centro. Logo, o arco MSN vale 60º. Eis o desenho:
- geomcirc.JPG (11.21 KiB) Exibido 4673 vezes
-
Douglasm
- Colaborador Voluntário
-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
por rafaelcb » Sex Out 01, 2010 03:17
Douglasm,
Muito OBRIGADO pela sua ajuda, sou muito agradecido
Abraço
Rafael
-
rafaelcb
- Novo Usuário
-
- Mensagens: 2
- Registrado em: Qui Set 30, 2010 12:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Psicologia
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (MACK) Em [0, 2?], se...
por manuoliveira » Ter Jun 01, 2010 21:02
- 2 Respostas
- 2613 Exibições
- Última mensagem por Mathmatematica
Dom Jun 06, 2010 21:22
Binômio de Newton
-
- Mack-SP
por -Sarah- » Sáb Fev 23, 2013 18:56
- 4 Respostas
- 2816 Exibições
- Última mensagem por -Sarah-
Ter Fev 26, 2013 20:20
Funções
-
- mack
por fna » Qua Jun 12, 2013 08:53
- 0 Respostas
- 888 Exibições
- Última mensagem por fna
Qua Jun 12, 2013 08:53
Geometria Plana
-
- Questão MACK-SP
por Diego Math » Qui Set 13, 2012 19:11
- 2 Respostas
- 8468 Exibições
- Última mensagem por Nina Luizet
Sáb Jun 13, 2015 16:02
Geometria Plana
-
- (MACK-SP) Função do 1º Grau
por 13run0 » Qui Mai 27, 2010 17:54
- 4 Respostas
- 2811 Exibições
- Última mensagem por 13run0
Sex Mai 28, 2010 14:15
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.
Em
substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.
2)Na equação
não existem zeros.Senão vejamos
Completando o quadrado,
As coordenadas do vertice da parabola são
O eixo de simetria é a reta
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
