poligonos convexos

[alfabeta]

ABCDEF... é um polígono convexo regular. Determine o número de lados do polígono, sabendo que o ângulo CÊF mede 144°.

Não sei montar a figura

[LuizAquino]

ABCDEF... é um polígono convexo regular. Determine o número de lados do polígono, sabendo que o ângulo CÊF mede 144°.

Não sei montar a figura

Basta montar uma figura como a que segue abaixo.

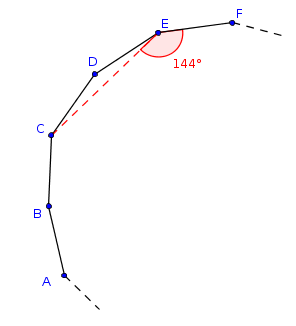
figura.png (5.23 KiB) Exibido 4104 vezes

Note que antes de A e depois de F nós colocamos segmentos tracejados para indicar que o polígono regular continua a partir dali.

[alfabeta]

Entendi a figura, muito obrigado. Mas continuo sem saber como encontrar o número de lados.
Sei a fórmula da soma dos ângulos internos de um polígono regular= 180(n-2).

[LuizAquino]

Entendi a figura, muito obrigado. Mas continuo sem saber como encontrar o número de lados.
Sei a fórmula da soma dos ângulos internos de um polígono regular= 180(n-2).

Dicas

Na figura que indiquei acima, CDE é um triângulo isósceles, pois CD e DE são lados de um polígono regular.

Além disso, temos que , pois e são ângulos internos de um polígono regular.

Com base nessas informações, você pode determinar quanto vale os ângulos internos desse polígono. A partir disso, fica fácil obter o número de lados.

[alfabeta]

Perfeito! Valeu!