 por Rosana Vieira » Qui Fev 16, 2012 22:56
por Rosana Vieira » Qui Fev 16, 2012 22:56
Olá será que alguém pode me ajudar a resolver este exercício, pois não conseguir colar a figura.
1)O uso de malhas quadriculadas contribui sobremaneira para a investigação de áreas de figuras, inclusive as mais complexas.
a) Com auxílio de malhas quadriculadas encontre uma aproximação razoável para a área de um círculo de raio igual a 6 cm. Determine qual foi a aproximação (%) obtida.
b) Faça o mesmo para encontrar uma aproximação para a área da região plana limitada pela elipse da figura abaixo, cuja equação reduzida é: , x e y reais, e .
-
Rosana Vieira
- Usuário Parceiro

-
- Mensagens: 74
- Registrado em: Qui Nov 17, 2011 00:11
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por fraol » Qui Fev 16, 2012 23:22
por fraol » Qui Fev 16, 2012 23:22
Se entendi, está se querendo usar malha quadriculada para aproximação de áreas como instrumentação do ensino. Adicionei uma figura no final desta mensagem.
a) Com auxílio de malhas quadriculadas encontre uma aproximação razoável para a área de um círculo de raio igual a 6 cm. Determine qual foi a aproximação (%) obtida.
Na figura usei quadradinhos de lado valendo 0.5 um (unidade de medida), logo cada quadradinho tem área igual a
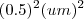
. Assim para aproximar a área do círculo de raio = 6 um, basta contar a quantidade de quadradinhos que compõe o círculo. Quanto menor o lado de cada quadradinho, maior o número de quadradinhos na malha e por conseguinte melhor é a aproximação da área ( haja paciência para contar os tais quadradinhos! ).
Para calcular o % de aproximação você pode dividir a área "contada" em quadradinhos pela área do círculo (
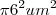
e multiplicar por 100.
b) Faça o mesmo para encontrar uma aproximação para a área da região plana limitada pela elipse da figura abaixo, cuja equação reduzida é: , x e y reais, e .
Usar um mecanismo análogo.

- malha
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Rosana Vieira » Sex Fev 17, 2012 00:41
por Rosana Vieira » Sex Fev 17, 2012 00:41
[quote="Rosana Vieira"]Olá será que alguém pode me ajudar a resolver este exercício, pois não conseguir colar a figura.
1)O uso de malhas quadriculadas contribui sobremaneira para a investigação de áreas de figuras, inclusive as mais complexas.
a) Com auxílio de malhas quadriculadas encontre uma aproximação razoável para a área de um círculo de raio igual a 6 cm. Determine qual foi a aproximação (%) obtida.
b) Faça o mesmo para encontrar uma aproximação para a área da região plana limitada pela elipse da figura abaixo, cuja equação reduzida é: , x e y reais, é x2/36 + y2/16 = 1, x e y reais, -6menor igual x menor igual 6 e - 4menor igual y menor igual 4.
(Lembramos que a área da região plana limitada por uma elipse com semi-eixos a e b é obtida pelo produto . Veja que, neste caso, a = 6 e b = 4).
-
Rosana Vieira
- Usuário Parceiro

-
- Mensagens: 74
- Registrado em: Qui Nov 17, 2011 00:11
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- geometria espacial
por Gir » Seg Jul 27, 2009 11:46
- 3 Respostas
- 11744 Exibições
- Última mensagem por Molina

Ter Jul 28, 2009 15:21
Problemas do Cotidiano
-
- Geometria espacial
por nathy vieira » Qua Out 07, 2009 22:37
- 2 Respostas
- 2860 Exibições
- Última mensagem por nathy vieira

Qua Out 07, 2009 23:03
Geometria Espacial
-
- geometria espacial
por nathy vieira » Qua Out 07, 2009 23:18
- 4 Respostas
- 6160 Exibições
- Última mensagem por nathy vieira

Qui Out 08, 2009 18:37
Geometria Espacial
-
- Geometria espacial
por crixprof » Qui Out 15, 2009 10:40
- 2 Respostas
- 3169 Exibições
- Última mensagem por crixprof

Sex Out 16, 2009 18:27
Geometria Espacial
-
- Geometria Espacial
por geriane » Sáb Abr 03, 2010 10:39
- 4 Respostas
- 4213 Exibições
- Última mensagem por geriane

Dom Abr 04, 2010 10:29
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


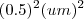 . Assim para aproximar a área do círculo de raio = 6 um, basta contar a quantidade de quadradinhos que compõe o círculo. Quanto menor o lado de cada quadradinho, maior o número de quadradinhos na malha e por conseguinte melhor é a aproximação da área ( haja paciência para contar os tais quadradinhos! ).
. Assim para aproximar a área do círculo de raio = 6 um, basta contar a quantidade de quadradinhos que compõe o círculo. Quanto menor o lado de cada quadradinho, maior o número de quadradinhos na malha e por conseguinte melhor é a aproximação da área ( haja paciência para contar os tais quadradinhos! ).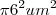 e multiplicar por 100.
e multiplicar por 100. 


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.